
С����ѧϰ������֪ʶʱ����������������Ȥ�Ľ��ۣ���Rt��ABC�У���A=90�㣬BDƽ����ABC��MΪֱ��AC��һ�㣬ME��BC������ΪE����AME��ƽ���߽�ֱ��AB�ڵ�F��
��1����ͼ�٣�MΪ��AC��һ�㣬��BD��MF��λ����ϵ�� ��
��ͼ�ڣ�MΪ��AC�����ӳ�����һ�㣬��BD��MF��λ�ù�ϵ�� ��
��ͼ�ۣ�MΪ��AC�ӳ�����һ�㣬��BD��MF��λ�ù�ϵ�� ��
��2�����ͼ�١�ͼ�ڡ���ͼ���е�һ�����������֤����
��ѡͼ ��֤����

��1��BD��MF��BD��MF��BD��MF����2��֤����������
��������
�����������1������������֪��AME+��ABC=180�㣬�����ý�ƽ���ߵ����ʵá�AMF+��ABD=90��,����AMF+��AFM=90��,�Ӷ���AFM=��ABD����BD��MF��
����֤��AME=��ABC,��MF��BD�ֱ��ǡ�AME����ABC��ƽ���ߣ���֪��AMF=��ABD������ABD+��ADB=90�㣬���ԡ�AMF+��ADB=90�㣬��BD��MF��
������ͬ��2����
(2)����ͬ��1����
(1) BD��MF��BD��MF��BD��MF��
(2) ��1��BD��MF
�������£��ߡ�A=90�㣬ME��BC��
���ABC+��AME=360�㩁90���2=180�㣬
��BDƽ�֡�ABC��MFƽ�֡�AME��
���ABD=��ABC����AMF=��AME��
���ABD+��AMF=����ABC+��AME��=90�㣬
�֡ߡ�AFM+��AMF=90�㣬
���ABD=��AFM��
��BD��MF��
��2��BD��MF��
�������£��ߡ�A=90�㣬ME��BC��
���ABC+��C=��AME+��C=90�㣬
���ABC=��AME��
��BDƽ�֡�ABC��MFƽ�֡�AME��
���ABD=��AMF��
�ߡ�ABD+��ADB=90�㣬
���AMF+��ADB=90�㣬
��BD��MF��
��3��BD��MF��
�������£��ߡ�A=90�㣬ME��BC��
���ABC+��ACB=��AME+��ACB=90�㣬
���ABC=��AME��
��BDƽ�֡�ABC��MFƽ�֡�AME��
���ABD=��AMF��
�ߡ�AMF+��F=90�㣬
���ABD+��F=90�㣬
��BD��MF
������1��ƽ���ߵ��ж���2����ֱ���ж���3���ı��ε��ڽǺ���


 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016�콭��ʡ�γ��ж�̨�����꼶��ѧ�ڵ�һ���¿���ѧ�Ծ��������棩 ���ͣ������
һ�����������ε����߳��ֱ���3cm��7cm���������ܳ��� cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016�콭��ʡ���������꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ�ѡ����
����ͼ���У���AB��CD���ܵõ���1=��2���ǣ� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016�콭��ʡ�����б��������꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
���㣺(xy)5��(xy)3��_____________������0.25��2013��42014��____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016�콭��ʡ�����б��������꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ�ѡ����
����Ϊ3cm��6cm��8cm��9cm�������߶Σ��������е������߶�Ϊ�߹��������Σ����Թ��ɲ�ͬ�������ι��� �� ��
A��1�� B��2�� C��3�� D��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016�콭��ʡ�����г簲�����꼶��ѧ������ͳ����ѧ�Ծ��������棩 ���ͣ������
�Ȼ�������ֵ��2(x��1)(x-1)-3x(3��x)��(x��5)(x-2)������x=- ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016�콭��ʡ�����г簲�����꼶��ѧ������ͳ����ѧ�Ծ��������棩 ���ͣ������
���(x��2)(x��p)�ij˻�����һ�����ôp= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016�콭��ʡ���������꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
(1)��֪(a-b)2=15��(a+b)2=7������ab��ֵ��
(2)�Ķ�����������
��֪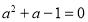 ����
����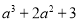 ��ֵ��
��ֵ��
��������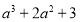
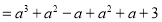
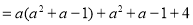
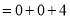

����������Ϸ�������������⣺
���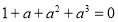 ���������ʽ
���������ʽ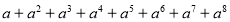 ��ֵ
��ֵ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com