
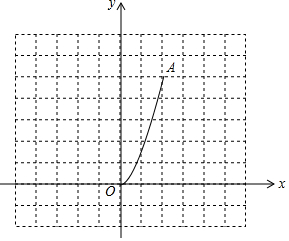
 如图,二次函数y=$\frac{5}{4}$x2(0≤x≤2)的图象记为曲线C1,将C1绕坐标原点O逆时针旋转90°,得曲线C2.
如图,二次函数y=$\frac{5}{4}$x2(0≤x≤2)的图象记为曲线C1,将C1绕坐标原点O逆时针旋转90°,得曲线C2. 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
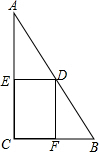 如图,在Rt△ABC中,已知∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F.得四边形DECF.设DE=x,DF=y
如图,在Rt△ABC中,已知∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F.得四边形DECF.设DE=x,DF=y查看答案和解析>>
科目:初中数学 来源: 题型:解答题
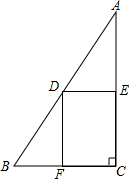 如图,在Rt△ABC中,∠C=90°,BC=6,AC=12,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为点E,F,得四边形DECF,设DE=x,DF=y.
如图,在Rt△ABC中,∠C=90°,BC=6,AC=12,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为点E,F,得四边形DECF,设DE=x,DF=y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
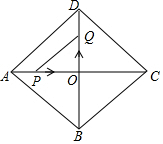 如图,在菱形ABCD中,AD=5,AC=8,对角线AC,BD交于点O,P,Q分别是线段AO,DO上的动点,P从A出发以1cm/s的速度向O运动,Q从点O出发以2cm/s的速度向点D运动,设运动时间为t,四边形APQD面积为y.
如图,在菱形ABCD中,AD=5,AC=8,对角线AC,BD交于点O,P,Q分别是线段AO,DO上的动点,P从A出发以1cm/s的速度向O运动,Q从点O出发以2cm/s的速度向点D运动,设运动时间为t,四边形APQD面积为y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 平板电脑 | PC机 | |
| 进价(元/台) | 5400 | 3500 |
| 售价(元/台) | 6100 | 3900 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com