
分析 根据根与系数的关系可得出m+n=$\frac{3}{2}$、mn=$\frac{1}{2}$,将$\frac{1}{m}$+$\frac{1}{n}$统分后代入数据即可得出结论.
解答 解:∵m,n是方程2x2-3x+1=0的两根,
∴m+n=$\frac{3}{2}$,mn=$\frac{1}{2}$,
∴$\frac{1}{m}$+$\frac{1}{n}$=$\frac{m+n}{mn}$=$\frac{\frac{3}{2}}{\frac{1}{2}}$=3.
故答案为:3.
点评 本题考查了根与系数的关系,熟练掌握“x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$”是解题的关键.


科目:初中数学 来源: 题型:填空题
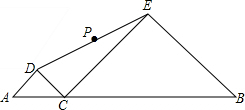 如图,线段AB长为6,点C是线段AB上一动点(不与A,B重合)分别以AC和BC为斜边,在AB的同侧作等腰直角三角形△ADC,△CEB,点P是DE的中点,当点C从距离A点1处沿AB向右运动至距离B点1处时,点P运动的路径长是2.
如图,线段AB长为6,点C是线段AB上一动点(不与A,B重合)分别以AC和BC为斜边,在AB的同侧作等腰直角三角形△ADC,△CEB,点P是DE的中点,当点C从距离A点1处沿AB向右运动至距离B点1处时,点P运动的路径长是2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x-1+y-1 | B. | $\frac{1}{xy}$ | C. | $\frac{1}{x}$+$\frac{1}{y}$ | D. | $\frac{1}{x+y}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 任何数都有两个平方根 | B. | 若a>0,x2=a,则x是a的一个平方根 | ||
| C. | 2的平方根是4 | D. | 若a>0,x2=a,则a是x的一个平方根 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
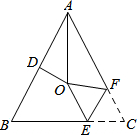 如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数是( )
如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数是( )| A. | 106° | B. | 108° | C. | 110° | D. | 112° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
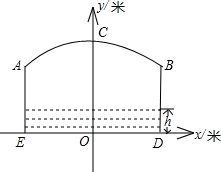 如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE、ED、DB组成,已知河底ED是水平的,ED=16米,AE=8米,抛物线的顶点C到ED的距离是11米,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.
如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE、ED、DB组成,已知河底ED是水平的,ED=16米,AE=8米,抛物线的顶点C到ED的距离是11米,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com