
【题目】在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上,
上,![]() ,点
,点![]() 在线段
在线段![]() 上,
上,![]() 是
是![]() 的中点,直线
的中点,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(1)如图,若点![]() 在线段
在线段![]() 上,线段
上,线段![]() 和
和![]() 之间的数量关系是 ,位置关系是 ;
之间的数量关系是 ,位置关系是 ;
(2)在(1)的条件下,当点![]() 在线段
在线段![]() 上,且
上,且![]() 时,求证:
时,求证:![]() ;
;
(3)当点![]() 在线段
在线段![]() 的延长线上时,在线段
的延长线上时,在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.

【答案】(1)![]() ,
,![]() ;(2)见解析;(3)存在,
;(2)见解析;(3)存在,![]() ,理由见解析
,理由见解析
【解析】
(1)通过证△AEC≌△CMB,得到AE=CM并得到∠ACM+∠BCM=90°,进而推导出AE⊥CM;
(2)如图1,在Rt△ABC中,求得AB=12,再通过勾股定理及中位线定理,可得到FM=FG=5;
(3)将![]() 绕点
绕点![]() 逆时针旋转90°得
逆时针旋转90°得![]() ,构造全等△三角形(
,构造全等△三角形(![]() ),再证
),再证![]() ,最后在Rt△PBF中利用勾股定理得求GF,进而求得AF.
,最后在Rt△PBF中利用勾股定理得求GF,进而求得AF.
(1)![]()
![]() 如图1,延长
如图1,延长![]() 交
交![]() 于点H.
于点H.
∵![]() ,
,![]() ,
,![]() 于点
于点![]() ,
,
∴![]() ,
,![]() .
.
∵![]() 是
是![]() 的中点,∴
的中点,∴![]() .∴
.∴![]()
∴![]() .
.
在![]() 和
和![]() 中,
中,
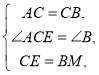 ∴
∴![]() (
(![]() ).
).
∴![]() ,
,![]() .∵
.∵![]()
∴![]() .
.
∴![]() ,∴
,∴![]() .
.
(2)解:如图1,过点![]() 作
作![]() ,且
,且![]() ,连接CG,
,连接CG,![]() ,延长
,延长![]() 交
交![]() 于点H.
于点H.
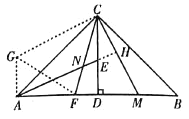
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
∵![]() ,
,![]() .
.
∵![]() 是
是![]() 的中点,∴
的中点,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
在![]() 和△BCM中
和△BCM中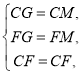
∴![]() ,
,
∴![]() .
.
由(1),知![]() , ∴
, ∴![]() ,
,
∴![]() .
.
(3)解:存在.![]() .理由如下:
.理由如下:
方法一:如图2,取![]() 中点
中点![]() ,连接CG并延长交
,连接CG并延长交![]() 于点H,将
于点H,将![]() 绕点
绕点![]() 逆时针旋转90°得
逆时针旋转90°得![]() ,连接
,连接![]() ,则
,则![]() .可证
.可证![]() ,∴
,∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
由旋转,知![]() ,∴
,∴![]() ,
,
∴![]() .
.
又∵![]() ,
,![]() ,∴,
,∴,
∴![]() .
.
设![]() ,则
,则![]() ,
,![]() .
.
在Rt△PBF中,![]() ,解得
,解得![]() .
.
∴![]() .
.
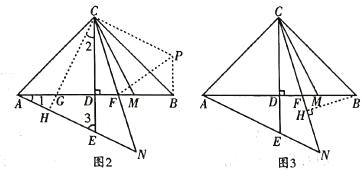
方法二:如图3,作![]() 于点H.
于点H.
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,∴DE=3.
,∴DE=3.
在Rt△ADE中,由勾股定理,得![]() ,
,
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() ,
,
∴![]() ,即
,即![]() ,解得
,解得![]() .
.
设![]() ,则
,则![]() .
.
在![]() 中,由勾股定理,得
中,由勾股定理,得
![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即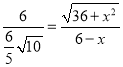 ,
,
解得![]() ,
,![]() (舍去).
(舍去).
∴![]() .∴
.∴![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的内接三角形,
的内接三角形,![]() 的角平分线
的角平分线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作直线
作直线![]() .
.

(1)判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若在![]() 上取一点
上取一点![]() 使
使![]() ,求证:
,求证:![]() 是
是![]() 的平分线;
的平分线;
(3)在(2)的条件下,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰![]() 中,
中,![]() ,
,![]() .动点
.动点![]() 在
在![]() 上以每分钟5个单位长度的速度从
上以每分钟5个单位长度的速度从![]() 点出发向
点出发向![]() 点移动,过
点移动,过![]() 作
作![]() 交
交![]() 边于
边于![]() 点,连结
点,连结![]() 、
、![]() .设
.设![]() 点移动的时间为
点移动的时间为![]() .
.
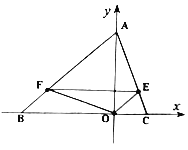
(1)求![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)计算:当![]() 面积最大时,
面积最大时,![]() 的值;
的值;
(3)在(2)的条件下,边![]() 上是否还存在一个点
上是否还存在一个点![]() ,使得
,使得![]() ?若存在,请直接写出
?若存在,请直接写出![]() 点的坐标;若不存在,试说明理由.
点的坐标;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(﹣1,0)、(0,﹣3).
(1)求抛物线的函数解析式;
(2)点E为抛物线的顶点,点C为抛物线与x轴的另一交点,点D为y轴上一点,且DC=DE,求出点D的坐标;
(3)在第二问的条件下,在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,请你直接写出所有满足条件的点P的坐标.
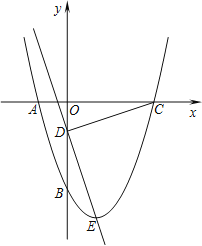
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
(1)求证:直线CP是⊙O的切线.
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求点B到AC的距离.
,求点B到AC的距离.
(3)在第(2)的条件下,求△ACP的周长.
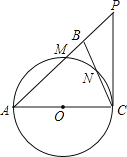
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,DEF分别为△ABC边ACABBC上的点,∠A=∠1=∠C,DE=DF.下面的结论一定成立的是( )
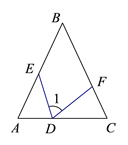
A. AE=FC B. AE=DE C. AE+FC=AC D. AD+FC=AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一笔直的公路连接![]() 、
、![]() 两地,甲车从
两地,甲车从![]() 地驶往
地驶往![]() 地,速度为每小时60千米,同时乙车从
地,速度为每小时60千米,同时乙车从![]() 地驶往
地驶往![]() 地,速度为每小时80千米.途中甲车发生故障,于是停车修理了2.5小时,修好后立即开车驶往
地,速度为每小时80千米.途中甲车发生故障,于是停车修理了2.5小时,修好后立即开车驶往![]() 地.设甲车行驶的时间为
地.设甲车行驶的时间为![]() ,两车之间的距离为
,两车之间的距离为![]() .已知
.已知![]() 与
与![]() 的函数关系的部分图像如图所示.
的函数关系的部分图像如图所示.
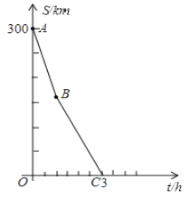
(1)直接写出![]() 点的实际意义.
点的实际意义.
(2)问:甲车出发几小时后发生故障?
(3)将![]() 与
与![]() 的函数图象补充完整.(请对画出的图象用数据作适当的标注)
的函数图象补充完整.(请对画出的图象用数据作适当的标注)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 分别在
分别在![]() 两边上,且
两边上,且![]() ,以
,以![]() 为直径作半圆
为直径作半圆![]() ,点
,点![]() 是半圆
是半圆![]() 的中点
的中点
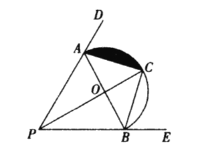
(1)连接![]() ,求证:
,求证: ![]() ;
;
(2)若![]() ,
, ![]() ,求阴影部分面积
,求阴影部分面积
(3)若点![]() 是
是![]() 的外心,判断四边形
的外心,判断四边形![]() 的形状,并说明理由
的形状,并说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com