
ΓΨΧβΡΩΓΩ‘ΎRtΓςABC÷–Θ§ΓœBAC=90ΓψΘ§BC=10Θ§tanΓœABC=![]() Θ§ΒψO «AB±Ώ…œΕ·ΒψΘ§“‘OΈΣ‘≤–ΡΘ§OBΈΣΑκΨΕΒΡΓ―O”κ±ΏBCΒΡΝμ“ΜΫΜΒψΈΣDΘ§ΙΐΒψDΉςABΒΡ¥ΙœΏΘ§ΫΜΓ―O”ΎΒψEΘ§ΝΣΫαBEΓΔAE
Θ§ΒψO «AB±Ώ…œΕ·ΒψΘ§“‘OΈΣ‘≤–ΡΘ§OBΈΣΑκΨΕΒΡΓ―O”κ±ΏBCΒΡΝμ“ΜΫΜΒψΈΣDΘ§ΙΐΒψDΉςABΒΡ¥ΙœΏΘ§ΫΜΓ―O”ΎΒψEΘ§ΝΣΫαBEΓΔAE
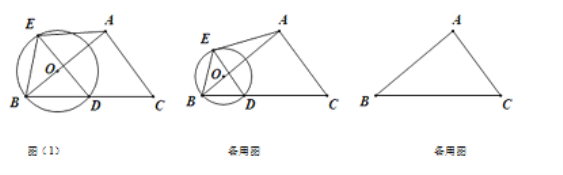
Θ®1Θ©»γΆΦΘ®1Θ©Θ§Β±AEΓΈBC ±Θ§«σΓ―OΒΡΑκΨΕ≥ΛΘΜ
Θ®2Θ©…ηBO=xΘ§AE=yΘ§«σyΙΊ”ΎxΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ–¥≥ωΕ®“ε”ρΘΜ
Θ®3Θ©»τ“‘AΈΣ‘≤–ΡΒΡΓ―A”κΓ―O”–ΙΪΙ≤ΒψDΓΔEΘ§Β±Γ―A«ΓΚΟ“≤ΙΐΒψC ±Θ§«σDEΒΡ≥ΛΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©Γ―OΒΡΑκΨΕ≥ΛΈΣ![]() ΘΜΘ®2Θ©y =
ΘΜΘ®2Θ©y =![]() Θ§Ε®“ε”ρΘ®0ΘΦxΓή
Θ§Ε®“ε”ρΘ®0ΘΦxΓή![]() Θ©ΘΜΘ®3Θ©Β±Γ―A«ΓΚΟ“≤ΙΐΒψC ±Θ§DEΒΡ≥ΛΈΣ
Θ©ΘΜΘ®3Θ©Β±Γ―A«ΓΚΟ“≤ΙΐΒψC ±Θ§DEΒΡ≥ΛΈΣ![]() Μρ12Θ°
Μρ12Θ°
ΓΨΫβΈωΓΩ
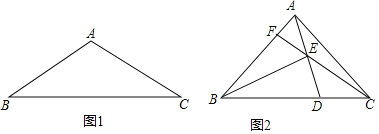
Θ®1Θ©»γΆΦ1÷–Θ§ΙΐΒψOΉςOGΓΆBD”ΎG…ηAB”κDEΒΡΫΜΒψΈΣFΘ° Ήœ»÷ΛΟςAEΘΫBDΘΫDCΘΫ10Θ§‘Όάϊ”Ο¥ΙΨΕΕ®άμ«σ≥ωBGΘ§‘ΎRtΓςBOD÷–Θ§Ϋβ÷±Ϋ«»ΐΫ«–ΈΦ¥Ω…ΘΜ
Θ®2Θ©»γΆΦ2÷–Θ§ΙΐΒψAΉςAHΓΆBC”ΎHΘ§»γΆΦΘ®2Θ©Θ§ Ήœ»«σ≥ωABΓΔACΓΔAHΘ§ΗυΨίyΘΫAEΘΫADΘΫ![]() Θ§Φ¥Ω…ΫβΨωΈ ΧβΘΜ
Θ§Φ¥Ω…ΫβΨωΈ ΧβΘΜ
Θ®3Θ©Ζ÷ΝΫ÷÷«ι–ΈΔΌ»τΒψD‘ΎHΒΡΉσ±ΏΘ§»γΆΦΘ®2Θ©Θ§ΔΎ»τΒψD‘ΎHΒΡ”“±ΏΘ§Ζ÷±π«σΫβΦ¥Ω…ΫβΨωΈ ΧβΘ°
Θ®1Θ©ΙΐΒψOΉςOGΓΆBD”ΎGΘ§…ηAB”κDEΒΡΫΜΒψΈΣFΘ§»γΆΦΘ®1Θ©Θ§
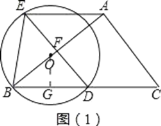
ΓΏOGΓΆBD”ΎGΘ§
ΓύBG=DGΘ°
ÿDEâABȧ
ΓύEF=DFΘ§
ÿAEøBCȧ
ΓύΓœAEF=ΓœBDFΘ°
‘ΎΓςAEFΚΆΓςBDF÷–Θ§
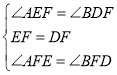 Θ§
Θ§
ΓύΓςAEFΓ’ΓςBDFΘ§
ΓύAE=BDΘ°
ΓΏΓœBFD=ΓœBAC=90ΓψΘ§
ΓύDEΓΈACΘ°
ÿAEøBCȧ
ΓύΥΡ±Ώ–ΈAEDC «ΤΫ––ΥΡ±Ώ–ΈΘ§
ΓύAE=DCΘ§
ΓύBD=DC=![]() BC=5Θ§
BC=5Θ§
ΓύBG=DG=![]() BD=
BD=![]() Θ°
Θ°
‘ΎRtΓςBGO÷–Θ§
tanΓœOBG=![]() =
=![]() Θ§
Θ§
ΓύOG=![]() BG=
BG=![]() ΓΝ
ΓΝ![]() =
=![]() Θ§
Θ§
ΓύOB=![]() =
=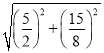 =
=![]() Θ§
Θ§
ΓύΓ―OΒΡΑκΨΕ≥ΛΈΣ![]() ΘΜ
ΘΜ
Θ®2Θ©ΙΐΒψAΉςAHΓΆBC”ΎHΘ§»γΆΦΘ®2Θ©Θ§
‘ΎRtΓςBAC÷–Θ§
tanΓœABC=![]() =
=![]() Θ§
Θ§
…ηAC=3kΘ§‘ρAB=4kΘ§
ΓύBC=5k=10Θ§
Γύk=2Θ§
ΓύAC=6Θ§AB=8Θ§
ΓύAH=![]() =
=![]() =
=![]() Θ§
Θ§
ΓύBH=![]() =
=![]() Θ§
Θ§
ΓύHC=BC©¹BH=10©¹![]() =
=![]() Θ°
Θ°
ÿABâDEȧ
ΓύΗυΨί¥ΙΨΕΕ®άμΩ…ΒΟDF=EFΘ§
ΓύAB¥Ι÷±ΤΫΖ÷DEΘ§
ΓύAE=ADΘ°
‘ΎRtΓςBGO÷–Θ§
tanΓœOBG=![]() =
=![]() Θ§
Θ§
ΓύOG=![]() BGΘ§
BGȧ
ΓύOB=![]() =
=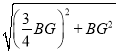 =
=![]() BG=xȧ
BG=xȧ
ΓύBG=![]() xΘ§
xȧ
ΓύBD=2BG=![]() xΘ§
xȧ
ΓύDH=BH©¹BD=![]() ©¹
©¹![]() xΘ§
xȧ
Γύy=AE=AD=![]() =
=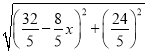 =
=![]()
Ε®“ε”ρΘ®0ΘΦxΓή![]() Θ©ΘΜ
Θ©ΘΜ
Θ®3Θ©ΔΌ»τΒψD‘ΎHΒΡΉσ±ΏΘ§»γΆΦΘ®2Θ©Θ§
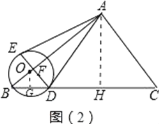
ÿAD=ACȧAHâDCȧ
ΓύDH=CH=![]() Θ§
Θ§
ΓύBD=BH©¹DH=![]() ©¹
©¹![]() =
=![]() Θ°
Θ°
‘ΎRtΓςBFD÷–Θ§
tanΓœFBD=![]() =
=![]() Θ§
Θ§
ΓύBF=![]() DFΘ§
DFȧ
ΓύBD=![]() =
=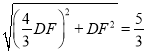 DF=
DF=![]() Θ§
Θ§
ΓύDF=![]() Θ§
Θ§
ΓύDE=2DF=![]() ΘΜ
ΘΜ
ΔΎ»τΒψD‘ΎHΒΡ”“±ΏΘ§
‘ρΒψD”κΒψC÷ΊΚœΘ§
ΓύBD=BC=10Θ§
Γύ![]() DF=10Θ§
DF=10Θ§
ΓύDF=6Θ§
ΓύDE=2DF=12Θ°
Ήέ…œΥυ ωΘΚΒ±Γ―A«ΓΚΟ“≤ΙΐΒψC ±Θ§DEΒΡ≥ΛΈΣ![]()


 Ά§≤ΫΝΖœΑΚ”Ρœ¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ
Ά§≤ΫΝΖœΑΚ”Ρœ¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ Ά§≤ΫΝΖœΑΈςΡœ¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ
Ά§≤ΫΝΖœΑΈςΡœ¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ ≤Ι≥δœΑΧβΫ≠Υ’œΒΝ–¥πΑΗ
≤Ι≥δœΑΧβΫ≠Υ’œΒΝ–¥πΑΗ ―ßΝΖΩλ≥ΒΒάΩΎΥψ–ΡΥψΥΌΥψΧλΧλΝΖœΒΝ–¥πΑΗ
―ßΝΖΩλ≥ΒΒάΩΎΥψ–ΡΥψΥΌΥψΧλΧλΝΖœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ![]() ÷–Θ§
÷–Θ§![]() ΈΣœΏΕΈ
ΈΣœΏΕΈ![]() …œ“ΜΒψΘ§
…œ“ΜΒψΘ§![]() ΈΣ…δœΏ
ΈΣ…δœΏ![]() …œ“ΜΒψΘ§«“
…œ“ΜΒψΘ§«“![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ°
Θ°
(1)»γΆΦ1Θ§»τ![]() Θ§«κ≤Ι»ΪΆΦ–Έ≤Δ«σ
Θ§«κ≤Ι»ΪΆΦ–Έ≤Δ«σ![]() ΒΡ≥ΛΘΜ
ΒΡ≥ΛΘΜ
(2)»γΆΦ2Θ§»τ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() ≤Δ―”≥ΛΘ§ΫΜ
≤Δ―”≥ΛΘ§ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§–ΓΟςΆ®ΙΐΙέ≤λΓΔ Β―ιΧα≥ω≤¬œκΘΚ
Θ§–ΓΟςΆ®ΙΐΙέ≤λΓΔ Β―ιΧα≥ω≤¬œκΘΚ![]() Θ°–ΓΟςΑ―’βΗω≤¬œκ”κΆ§―ßΟ«Ϋχ––ΫΜΝςΘ§Ά®ΙΐΧ÷¬έΘ§–Έ≥…ΝΥ÷ΛΟςΗΟ≤¬œκΒΡΦΗ÷÷œκΖ®ΘΚ
Θ°–ΓΟςΑ―’βΗω≤¬œκ”κΆ§―ßΟ«Ϋχ––ΫΜΝςΘ§Ά®ΙΐΧ÷¬έΘ§–Έ≥…ΝΥ÷ΛΟςΗΟ≤¬œκΒΡΦΗ÷÷œκΖ®ΘΚ
œκΖ®1ΘΚΙΐ![]() Ής
Ής![]() ΫΜ
ΫΜ![]() ΒΡ―”≥ΛœΏ”ΎΒψ
ΒΡ―”≥ΛœΏ”ΎΒψ![]() Θ§œ»÷Λ≥ω
Θ§œ»÷Λ≥ω![]() Θ§‘Ό÷Λ≥ω
Θ§‘Ό÷Λ≥ω![]() «Β»―ϋ»ΐΫ«–ΈΦ¥Ω…ΘΜ
«Β»―ϋ»ΐΫ«–ΈΦ¥Ω…ΘΜ
œκΖ®2ΘΚΙΐ![]() Ής
Ής![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§œ»÷Λ≥ω
Θ§œ»÷Λ≥ω![]() Θ§‘Ό÷ΛΒψ
Θ§‘Ό÷ΛΒψ![]() ΈΣœΏΕΈ
ΈΣœΏΕΈ![]() ΒΡ÷–ΒψΦ¥Ω…Θ°
ΒΡ÷–ΒψΦ¥Ω…Θ°
«κΡψ≤ΈΩΦ…œΟφΒΡœκΖ®Θ§Αο÷ζ–ΓΟς÷ΛΟς![]() Θ°(“Μ÷÷ΖΫΖ®Φ¥Ω…)
Θ°(“Μ÷÷ΖΫΖ®Φ¥Ω…)
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
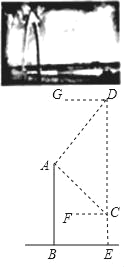
ΓΨΧβΡΩΓΩΆ®¥ο«≈Φ¥–ΓΒξΖΎΚ”«≈Θ§ «ΧΪ‘≠–¬Ϋ®≥…ΒΡ“ΜΉυΩγΖΎ¥σ«≈Θ§“≤ «ΧΪ‘≠ ΉΉυ–ϋΥς«≈Θ°«≈ΒΡ÷ςΥΰ”…«ζœΏ–ΈΙΑΟ≈Ήι≥…Θ§»Γ“βΓΑ ±¥ζ÷°Ο≈Γ±Θ°Έό»ΥΜζ…γΆ≈ΒΡΆ§―ßΦΤΜ°άϊ”ΟΈό»ΥΜζ…η±Η≤βΝΩΆ®¥ο«≈ΙΑΟ≈ΒΡΗΏΕ»Θ°»γΆΦΘ§ΥϊΟ«œ»ΫΪΈό»ΥΜζ…ΐ÷ΝΨύάκ«≈Οφ50ΟΉΗΏΒΡΒψC¥ΠΘ§≤βΒΟ«≈ΒΡΙΑΟ≈ΉνΗΏΒψAΒΡ―ωΫ«ΓœACFΈΣ30ΓψΘ§‘ΌΫΪΈό»ΥΜζ¥”C¥Π ζ÷±œρ…œ…ΐΗΏ200ΟΉΒΫΒψD¥ΠΘ§≤βΒΟΒψAΒΡΗ©Ϋ«ΓœADGΈΣ45ΓψΘ°“―÷ΣΒψAΘ§BΘ§CΘ§DΘ§E‘ΎΆ§“ΜΤΫΟφΡΎΘ§«σΆ®¥ο«≈ΙΑΟ≈ΉνΗΏΒψAΨύάκ«≈ΟφBEΒΡΗΏΕ»ABΘ°(ΫαΙϊ±ΘΝτ’ϊ ΐΘ§≤ΈΩΦ ΐΨίΘΚ![]() Γ÷1.41Θ§
Γ÷1.41Θ§![]() Γ÷1.73)
Γ÷1.73)
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
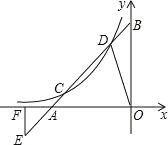
ΓΨΧβΡΩΓΩ“―÷Σ÷±œΏyΘΫx+3”κx÷αΓΔy÷αΖ÷±πΫΜ”ΎAΘ§BΒψΘ§”κyΘΫ![]() Θ®xΘΦ0Θ©ΒΡΆΦœσΫΜ”ΎCΓΔDΒψΘ§E «ΒψCΙΊ”ΎΒψAΒΡ÷––ΡΕ‘≥ΤΒψΘ§EFΓΆOA”ΎFΘ§»τΓςAODΒΡΟφΜΐ”κΓςAEFΒΡΟφΜΐ÷°ΚΆΈΣ
Θ®xΘΦ0Θ©ΒΡΆΦœσΫΜ”ΎCΓΔDΒψΘ§E «ΒψCΙΊ”ΎΒψAΒΡ÷––ΡΕ‘≥ΤΒψΘ§EFΓΆOA”ΎFΘ§»τΓςAODΒΡΟφΜΐ”κΓςAEFΒΡΟφΜΐ÷°ΚΆΈΣ![]() ±Θ§‘ρkΘΫ_____Θ°
±Θ§‘ρkΘΫ_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
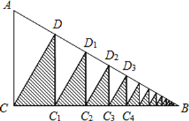
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎRtΓςABC÷–Θ§ΓœACB=90ΓψΘ§ΓœB=30ΓψΘ§AC=2Θ°ΉςΓςABCΒΡΗΏCDΘ§ΉςΓςCDBΒΡΗΏDC1Θ§ΉςΓςDC1BΒΡΗΏC1D1Θ§Γ≠Γ≠Θ§»γ¥Υœ¬»ΞΘ§Ρ«Ο¥ΒΟΒΫΒΡΥυ”–“θ”Α»ΐΫ«–ΈΒΡΟφΜΐ÷°ΚΆΈΣ__________.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§Ε·Βψ
Θ§Ε·Βψ![]() ¥”Βψ
¥”Βψ![]() ≥ωΖΔΘ§―Ί
≥ωΖΔΘ§―Ί![]() ÷α“‘ΟΩΟκ
÷α“‘ΟΩΟκ![]() ΗωΒΞΈΜΒΡΥΌΕ»œρ…œ“ΤΕ·Θ§«“ΙΐΒψ
ΗωΒΞΈΜΒΡΥΌΕ»œρ…œ“ΤΕ·Θ§«“ΙΐΒψ![]() ΒΡ÷±œΏ
ΒΡ÷±œΏ![]() “≤Υφ÷°“ΤΕ·Θ§»γΙϊΒψ
“≤Υφ÷°“ΤΕ·Θ§»γΙϊΒψ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΕ‘≥ΤΒψ¬δ‘ΎΉχ±ξ÷α…œΘ§ΟΜΒψ
ΒΡΕ‘≥ΤΒψ¬δ‘ΎΉχ±ξ÷α…œΘ§ΟΜΒψ![]() ΒΡ“ΤΕ· ±ΦδΈΣ
ΒΡ“ΤΕ· ±ΦδΈΣ![]() Θ§Ρ«Ο¥
Θ§Ρ«Ο¥![]() ΒΡ÷ΒΩ…“‘ «___.
ΒΡ÷ΒΩ…“‘ «___.
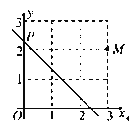
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΨΊ–ΈABCD÷–Θ§E «AB±ΏΒΡ÷–ΒψΘ§―ΊECΕ‘’έΨΊ–ΈABCDΘ§ ΙBΒψ¬δ‘ΎΒψP¥ΠΘ§’έΚέΈΣECΘ§ΝΣΫαAP≤Δ―”≥ΛAPΫΜCD”ΎFΒψΘ§
Θ®1Θ©«σ÷ΛΘΚΥΡ±Ώ–ΈAECFΈΣΤΫ––ΥΡ±Ώ–ΈΘΜ
Θ®2Θ©»γΙϊPA=PCΘ§ΝΣΫαBPΘ§«σ÷ΛΘΚΓςAPB![]() ΓςEPCΘ°
ΓςEPCΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
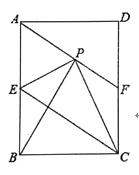
ΓΨΧβΡΩΓΩ–ΓΝ÷‘ΎΟΜ”–ΝΩΫ«ΤςΚΆ‘≤ΙφΒΡ«ιΩωœ¬Θ§άϊ”ΟΩΧΕ»≥ΏΚΆ“ΜΗ±»ΐΫ«ΑεΜ≠≥ωΝΥ“ΜΗωΫ«ΒΡΤΫΖ÷œΏΘ§ΥϊΒΡΉςΖ® «’β―υΒΡΘΚ»γΆΦ:
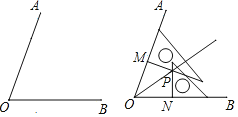
Θ®1Θ©άϊ”ΟΩΧΕ»≥Ώ‘ΎΓœAOBΒΡΝΫ±ΏOAΘ§OB…œΖ÷±π»ΓOMΘΫONΘΜ
Θ®2Θ©άϊ”ΟΝΫΗω»ΐΫ«ΑεΘ§Ζ÷±πΙΐΒψMΘ§NΜ≠OMΘ§ONΒΡ¥ΙœΏΘ§ΫΜΒψΈΣPΘΜ
Θ®3Θ©Μ≠…δœΏOPΘ°
‘ρ…δœΏOPΈΣΓœAOBΒΡΤΫΖ÷œΏΘ°«κ–¥≥ω–ΓΝ÷ΒΡΜ≠Ζ®ΒΡ“άΨί______Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΜΐΦΪœλ”Π –Έ·’ΰΗ°ΓΑΦ”ΩλΫ®…ηΧλάΕΥ°±ΧΒΊ¬ΧΒΡΟάάω≥Λ…≥Γ±ΒΡΚ≈’ΌΘ§Έ“ –Ρ≥Ϋ÷ΒάΨωΕ®¥”±Η―ΓΒΡΈε÷÷ ς÷–―ΓΙΚ“Μ÷÷Ϋχ––‘‘÷÷Θ°ΈΣΝΥΗϋΚΟΒΊΝΥΫβ…γ«ιΟώ“βΘ§ΙΛΉς»Υ‘±‘ΎΫ÷ΒάœΫ«χΖΕΈßΡΎΥφΜζ≥ι»ΓΝΥ≤ΩΖ÷Ψ”ΟώΘ§Ϋχ––ΓΑΈ“Ήνœ≤ΜΕΒΡ“Μ÷÷ ςΓ±ΒΡΒς≤ιΜνΕ·Θ®ΟΩ»Υœό―ΓΤδ÷–“Μ÷÷ ςΘ©Θ§≤ΔΫΪΒς≤ιΫαΙϊ’ϊάμΚσΘ§Μφ÷Τ≥…»γΆΦΝΫΗω≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘΚ

«κΗυΨίΥυΗχ–≈œΔΫβ¥π“‘œ¬Έ ΧβΘΚ
Θ®1Θ©’β¥Έ≤Έ”κΒς≤ιΒΡΨ”Οώ»Υ ΐΈΣΘΚ ΘΜ
Θ®2Θ©«κΫΪΧθ–ΈΆ≥ΦΤΆΦ≤Ι≥δΆξ’ϊΘΜ
Θ®3Θ©«κΦΤΥψ…»–ΈΆ≥ΦΤΆΦ÷–ΓΑΖψ ςΓ±Υυ‘Ύ…»–ΈΒΡ‘≤–ΡΫ«Ε» ΐΘΜ
Θ®4Θ©“―÷ΣΗΟΫ÷ΒάœΫ«χΡΎœ÷”–Ψ”Οώ8Άρ»ΥΘ§«κΡψΙάΦΤ’β8Άρ»Υ÷–Ήνœ≤ΜΕ”ώάΦ ςΒΡ”–Εύ…Ό»ΥΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com