
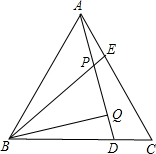
 如图,已知△ABC是等边三角形,且AE=CD,AD、BE相交于P,BQ⊥AD于Q.
如图,已知△ABC是等边三角形,且AE=CD,AD、BE相交于P,BQ⊥AD于Q.分析 (1)根据等边三角形的性质,通过全等三角形的判定定理SAS证得结论;
(2)利用(1)中的全等三角形的对应角相等和三角形外角的性质求得∠BPQ=60°;
(3)利用(2)的结果求得∠PBQ=30°,所以由“30度角所对的直角边是斜边的一半”得到2PQ=BP
解答 (1)证明:∵△ABC为等边三角形,
∴AB=CA,∠BAE=∠C=60°,
∴在△AEB与△CDA中,$\left\{\begin{array}{l}{AB=CA}\\{∠BAE=∠C}\\{AE=CD}\end{array}\right.$,
∴△AEB≌△CDA(SAS);
(2)解:由(1)知,△AEB≌△CDA,
∴∠ABE=∠CAD,
∴∠BAD+∠ABD=∠BAD+∠CAD=∠BAC=60°,
∴∠BPQ=∠BAD+∠ABD=60°;
∵BQ⊥AD,
∴∠PBQ=90°-∠BPQ=30°,
(3)解:如图,由(2)知,∠PBQ=30°,
∴PQ=$\frac{1}{2}$BP,
∴BP=2PQ.
点评 此题是全等三角形的判定与性质,主要考查了等边三角形的性质,含30度角的直角三角形.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件,此题是一道比较典型的题目,需记住这种题型的解决方法.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:解答题
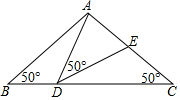 如图,在△ABC中,AB=AC=2,∠B=∠C=50°,点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=50°,DE交线段AC于E.
如图,在△ABC中,AB=AC=2,∠B=∠C=50°,点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=50°,DE交线段AC于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
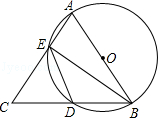 如图,△ABC中,AB=AC,以AB为直径的⊙O交AC,BC分别于点E,D两点,连结ED,BE.
如图,△ABC中,AB=AC,以AB为直径的⊙O交AC,BC分别于点E,D两点,连结ED,BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某人在山坡坡脚A处测得电视塔BC塔尖B的仰角为60°,沿山坡AM走到D处测得塔尖B的仰角为30°,已知AC为100米,山坡坡度i=1:3,C、A、E三点在同一直线上.求此人所在位置点D的铅直高度DE.(结果保留根号形式)
如图,某人在山坡坡脚A处测得电视塔BC塔尖B的仰角为60°,沿山坡AM走到D处测得塔尖B的仰角为30°,已知AC为100米,山坡坡度i=1:3,C、A、E三点在同一直线上.求此人所在位置点D的铅直高度DE.(结果保留根号形式)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,点E在CD边上,将矩形ABCD沿直线AE折叠,点D恰好落在BC边上的点F处.
如图,在矩形ABCD中,点E在CD边上,将矩形ABCD沿直线AE折叠,点D恰好落在BC边上的点F处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
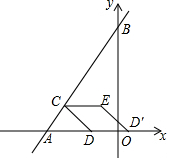 如图,在平面直角坐标系中,点A的坐标是(-3,0),点B的坐标是(0,4),动点C从点A出发沿射线AB方向以每秒1个单位的速度运动,过点C作CD⊥AB,交x轴于点D,点D关于y轴的对称点为D′,以DC,DD′为边作?CDD′E,设点C运动时间为t秒(t>0).
如图,在平面直角坐标系中,点A的坐标是(-3,0),点B的坐标是(0,4),动点C从点A出发沿射线AB方向以每秒1个单位的速度运动,过点C作CD⊥AB,交x轴于点D,点D关于y轴的对称点为D′,以DC,DD′为边作?CDD′E,设点C运动时间为t秒(t>0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com