
 如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )
如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 无数个 |
分析 如图在OA、OB上截取OE=OF=OP,作∠MPN=60°,只要证明△PEM≌△PON即可推出△PMN是等边三角形,由此即可对称结论.
解答 解:如图在OA、OB上截取OE=OF=OP,作∠MPN=60°.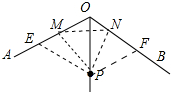
∵OP平分∠AOB,
∴∠EOP=∠POF=60°,
∵OP=OE=OF,
∴△OPE,△OPF是等边三角形,
∴EP=OP,∠EPO=∠OEP=∠PON=∠MPN=60°,
∴∠EPM=∠OPN,
在△PEM和△PON中,
$\left\{\begin{array}{l}{∠PEM=∠PON}\\{PE=PO}\\{∠EPM=∠OPN}\end{array}\right.$,
∴△PEM≌△PON.
∴PM=PN,
∵∠MPN=60°,
∴△PNM是等边三角形,
∴只要∠MPN=60°,△PMN就是等边三角形,
故这样的三角形有无数个,
故选D
点评 本题考查等边三角形的判定和性质、全等三角形的判定和性质、角平分线的性质等知识,解题的关键是正确添加辅助线,构造全等三角形,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
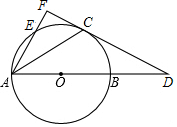 如图,AB是⊙O的直径,C为⊙O上一点,经过点C的直线与AB的延长线交于点D,连接AC,BC,∠BCD=∠CAB.E是⊙O上一点,弧CB=弧CE,连接AE并延长与DC的延长线交于点F.
如图,AB是⊙O的直径,C为⊙O上一点,经过点C的直线与AB的延长线交于点D,连接AC,BC,∠BCD=∠CAB.E是⊙O上一点,弧CB=弧CE,连接AE并延长与DC的延长线交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 39.8×105 | B. | 3.98×106 | C. | 3.98×107 | D. | 0.398×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | -2 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 检测矿区的空气质量 | |
| B. | 审查某篇文章中的错别字 | |
| C. | 调查全国七年级学生视力状况 | |
| D. | 调查山东电视台“我是大明星”的收视率 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ACB中,∠ACB=90°,AC=5cm,∠BAC=60°,动点M从点B出发,在边BA上以2cm/s的速度向点A匀速运动,同时动点N从点C出发,在边CB上以$\sqrt{3}$cm/s的速度向点B匀速运动,设运动时间为t s(0≤t≤5),连接MN.
如图,在Rt△ACB中,∠ACB=90°,AC=5cm,∠BAC=60°,动点M从点B出发,在边BA上以2cm/s的速度向点A匀速运动,同时动点N从点C出发,在边CB上以$\sqrt{3}$cm/s的速度向点B匀速运动,设运动时间为t s(0≤t≤5),连接MN.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com