
【题目】如图,在矩形![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 同时出发,点
同时出发,点![]() 以每秒
以每秒![]() 个单位长度的速度沿边
个单位长度的速度沿边![]() 向终点匀速运动,点
向终点匀速运动,点![]() 以每秒
以每秒![]() 个单位长度的速度沿边
个单位长度的速度沿边![]() 向终点匀速运动,以
向终点匀速运动,以![]() 为边在边
为边在边![]() 上方作正方形
上方作正方形![]() 设点
设点![]() 运动时间为
运动时间为![]() .
.
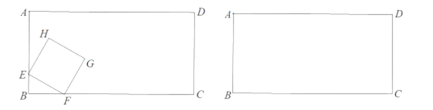
(1)用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)当点![]() 落在边
落在边![]() 上时,求此时
上时,求此时![]() 的值;
的值;
(3)设正方形![]() 与矩形
与矩形![]() 重叠图形的面积为
重叠图形的面积为![]() 请直接写出
请直接写出![]() 与
与![]() 之间的函数关系式,并写出
之间的函数关系式,并写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)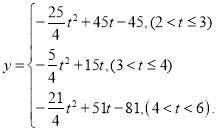
【解析】
(1)由题意可得BE,BF的长,由勾股定理即可求出EF;
(2)由四边形EFGH是正方形,易证得![]() ,进而得出
,进而得出![]() ,即可求得t的值;
,即可求得t的值;
(3)分![]() ,
,![]() ,
,![]() 三种情况进行分类讨论并画出图形,利用三角函数分别进行求解即可.
三种情况进行分类讨论并画出图形,利用三角函数分别进行求解即可.
(1) 由题意得,BE=t,BF=2t,
在Rt△BEF中,由勾股定理得,
![]() ,
,
(2)当点![]() 落在边
落在边![]() 上时,如图所示,
上时,如图所示,
过点![]() 作
作![]() 于点
于点![]()
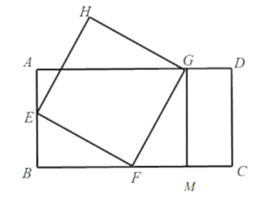
![]()
![]() 四边形
四边形![]() 为矩形,
为矩形,
![]()
∵四边形![]() 是正方形,
是正方形,
![]() ,
,
![]()
![]()
![]()
![]()
在![]() 与
与![]() 中
中
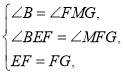
![]()
![]()
∵![]()
![]()
![]() ;
;
(3)①当![]() 时,如图,
时,如图,
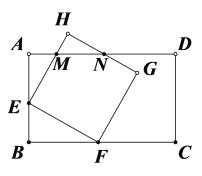
由题意得,BE=t,BF=2t,则AE=6-t,
∵四边形EFGH是正方形,
![]() ,
,
∴∠AEM+∠BEF=90°,∠BFE+∠BEF =90°,
∴∠BFE=∠AEM,
∴![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
∵四边形ABCD是矩形,四边形EFGH是正方形,
∴∠EAM=∠MHN=90°,
∵∠AME=∠HMN,
∴∠AEM=∠HNM
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ;
;
②当![]() 时,过点M作MP⊥FG,如图,
时,过点M作MP⊥FG,如图,
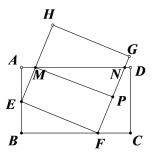
∵四边形EFGH是正方形,
∴∠HEF=∠GFE=90°,
∵MP⊥FG,
∴四边形MEFP是矩形,
∴∠EMP=90°,MP=EF=![]() ,
,
∴∠AME+∠PMN=90°,∠AEM+∠AME=90°,
∴∠AEM=∠PMN,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
③当![]() ,如图,
,如图,
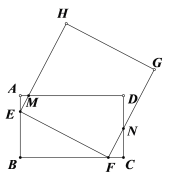
∵四边形EFGH是正方形,
∴∠EFG=90°,
∴∠BFE+∠NFC=90°,∠NFC+∠FNC =90°,
∴∠BFE =∠FNC,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
综上所述,正方形![]() 与矩形
与矩形![]() 重叠图形的面积为:
重叠图形的面积为:


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
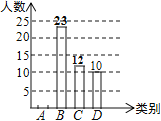
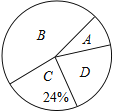
【题目】为弘扬中华传统文化,某校开展“双剧进课堂”的活动,该校童威随机抽取部分学生,按四个类别:![]() 表示“很喜欢”,
表示“很喜欢”,![]() 表示“喜欢”,
表示“喜欢”,![]() 表示“一般”,
表示“一般”,![]() 表示“不喜欢”,调查他们对汉剧的喜爱情况,将结果绘制成如下两幅不完整的统计图,根据图中提供的信息,解决下列问题:
表示“不喜欢”,调查他们对汉剧的喜爱情况,将结果绘制成如下两幅不完整的统计图,根据图中提供的信息,解决下列问题:
(1)这次共抽取_________名学生进行统计调查,扇形统计图中,![]() 类所对应的扇形圆心角的大小为__________
类所对应的扇形圆心角的大小为__________
(2)将条形统计图补充完整
(3)该校共有1500名学生,估计该校表示“喜欢”的![]() 类的学生大约有多少人?
类的学生大约有多少人?
各类学生人数条形统计图各类学生人数扇形统计图
查看答案和解析>>
科目:初中数学 来源: 题型:
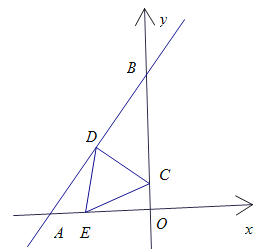
【题目】已知直线![]() 与
与![]() 轴相交于点A,与
轴相交于点A,与![]() 轴相交于点B.点C在
轴相交于点B.点C在![]() 轴上运动,作CD⊥AB,垂足为D.点E为
轴上运动,作CD⊥AB,垂足为D.点E为![]() 轴上一动点,点E关于CD中点的中心对称点为点F.设点C的坐标为(0,n).
轴上一动点,点E关于CD中点的中心对称点为点F.设点C的坐标为(0,n).
(1)用n表示线段CD的长;
(2)当OC=1时,若点F落在直线y轴上,求此时点E的坐标;
(3)在点E的运动过程中,若存在唯一的位置,使得四边形CEDF为矩形,请直接写出点C的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在任意四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() ,
,![]() 上的点,对于四边形
上的点,对于四边形![]() 的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
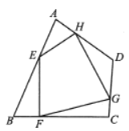
A.当![]() ,
,![]() ,
,![]() ,
,![]() 是各边中点,且
是各边中点,且![]() 时,四边形
时,四边形![]() 为菱形
为菱形
B.当![]() ,
,![]() ,
,![]() ,
,![]() 是各边中点,且
是各边中点,且![]() 时,四边形
时,四边形![]() 为矩形
为矩形
C.当![]() ,
,![]() ,
,![]() ,
,![]() 不是各边中点时,四边形
不是各边中点时,四边形![]() 可以为平行四边形
可以为平行四边形
D.当![]() ,
,![]() ,
,![]() ,
,![]() 不是各边中点时,四边形
不是各边中点时,四边形![]() 不可能为菱形
不可能为菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 经过
经过![]() ,
,![]() 两点.
两点.
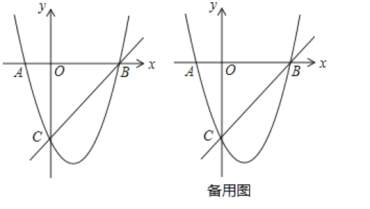
(1)求抛物线的解析式;
(2)过点![]() 作直线
作直线![]() 轴交抛物线于另一点
轴交抛物线于另一点![]() ,点
,点![]() 是直线
是直线![]() 下方抛物线上的一个动点,且在抛物线对称轴的右侧,过点
下方抛物线上的一个动点,且在抛物线对称轴的右侧,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 之间的函数解析式(不要求写出自变量
之间的函数解析式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)在(2)的条件下,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() (点
(点![]() 在线段
在线段![]() 上),
上),![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,当
,当![]() 时,求线段
时,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的方格纸中,△ABC的顶点都在小正方形的顶点上,以小正方形互相垂直的两边所在直线建立直角坐标系.

(1)作出△ABC关于y轴对称的△A1B1C1,其中点A,B,C分别和点A1,B1,C1对应;
(2)平移△ABC,使得点A在x轴上,点B在y轴上,平移后的三角形记为△A2B2C2,作出平移后的△A2B2C2,其中点A,B,C分别和点A2,B2,C2对应;
(3)直接写出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】CBA球赛已经开始,某体育用品商店预测某球队的球服能够畅销,就用![]() 万元购入了一批球服,上市后很快就脱销,该商店又用
万元购入了一批球服,上市后很快就脱销,该商店又用![]() 万元购入第二批该球队的球服,所购数量是第一批购入数量的2倍,但每套进价多了10 元.如果该商店购入的两批球服售价一样,且要求两批球服全部售完后总利润率不低于
万元购入第二批该球队的球服,所购数量是第一批购入数量的2倍,但每套进价多了10 元.如果该商店购入的两批球服售价一样,且要求两批球服全部售完后总利润率不低于![]() ,那么每套球服的售价至少是( )元.(利润率
,那么每套球服的售价至少是( )元.(利润率![]() 利润
利润![]() 成本
成本![]() )
)
A.160B.180C.200D.220
查看答案和解析>>
科目:初中数学 来源: 题型:
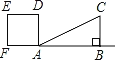
【题目】如图,Rt△ABC中,AB=4,BC=2,正方形ADEF的边长为2,F、A、B在同一直线上,正方形ADEF向右平移到点F与B重合,点F的平移距离为x,平移过程中两图重叠部分的面积为y,则y与x的关系的函数图象表示正确的是( )
A.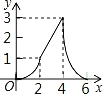 B.
B.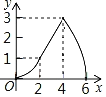
C.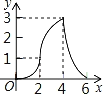 D.
D.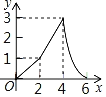
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店计划一次性购进甲、乙两种商品共![]() 件,甲、乙两种商品的进价和售价如下表所示:
件,甲、乙两种商品的进价和售价如下表所示:
甲 | 乙 | |
进价(元/件) | 100 | 80 |
售价(元/件) | 150 | 120 |
设购进甲种商品的数量为![]() 件.
件.
(1)设进货成本为![]() 元,求
元,求![]() 与
与![]() 之间的函数解析式;若购进甲种商品的数量不少于
之间的函数解析式;若购进甲种商品的数量不少于![]() 件,则最低进货成本是多少元?
件,则最低进货成本是多少元?
(2)若除了进货成本,还要支付运费和销售员工工资共![]() 元,为尽快回笼资金,该商店决定对甲种商品进行降价销售,每件甲种商品降价
元,为尽快回笼资金,该商店决定对甲种商品进行降价销售,每件甲种商品降价![]() 元
元![]() ,乙种商品售价不变,设销售完甲、乙两种商品获得的总利润为
,乙种商品售价不变,设销售完甲、乙两种商品获得的总利润为![]() 元.
元.
①每件甲种商品的利润是 元(用含![]() 的代数式表示)
的代数式表示)
②求![]() 关于
关于![]() 的函数解析式
的函数解析式
③当![]() 时,请你根据
时,请你根据![]() 的取值范围,说明该商店购进甲种商品多少件时,获得的总利润最大.
的取值范围,说明该商店购进甲种商品多少件时,获得的总利润最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com