
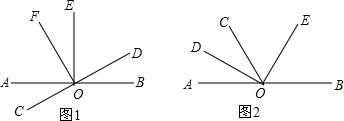
分析 (1)根据垂直的定义可以得到∠FOD=90°,即∠EOF+∠EOD=90°,然后根据∠EOF=∠DOB,即可求解;
(2)首先根据角平分线的定义求得∠AOD的度数,即可求得∠AOE的度数,则∠BOE即可求解.
解答 (1)证明:∵FO⊥CD,
∴∠FOD=90°,
即∠EOF+∠DOE=90°,
∵∠EOF=∠DOB,
∴∠DOB+∠EOD=90°,
EO⊥AB;
(2)解:∵OD平分∠AOC,
∴∠AOD=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×58°=29°,
∵∠AOB=180°,∠DOE=90°,
∴∠BOE=180°-90°-29°=61°.
点评 本题考查对顶角的性质以及邻补角的定义和垂直的定义,熟记定义是解答此题的关键.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:填空题
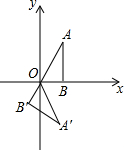 如图,点B在x轴上,∠ABO=90°,∠A=30°,OA=4,将△OAB绕点O按顺时针方向旋转120°得到△OA′B′,则点A′的坐标是(2,-2$\sqrt{3}$).
如图,点B在x轴上,∠ABO=90°,∠A=30°,OA=4,将△OAB绕点O按顺时针方向旋转120°得到△OA′B′,则点A′的坐标是(2,-2$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
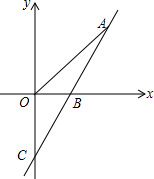 如图,直线y=kx-2与x轴,y轴分别交于点B,C,且OC=2OB,A为直线BC上一动点.
如图,直线y=kx-2与x轴,y轴分别交于点B,C,且OC=2OB,A为直线BC上一动点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
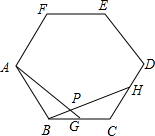 如图,点G,H分别是正六边形ABCDEF的边BC,CD上的点,且BG=CH,AG交BH于点P.(1)求证:△ABG≌△BCH;
如图,点G,H分别是正六边形ABCDEF的边BC,CD上的点,且BG=CH,AG交BH于点P.(1)求证:△ABG≌△BCH;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>n | B. | m<n | C. | m=n | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=$\frac{k}{x}$(k>0)的图象与BC边交于点E.
如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=$\frac{k}{x}$(k>0)的图象与BC边交于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com