
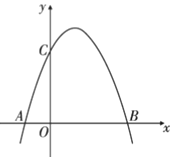
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴的交点为
轴的交点为![]() .
.
(1)求点![]() 和点
和点![]() 的坐标;
的坐标;
(2)若点![]() 为抛物线上一点,且
为抛物线上一点,且![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ;(2)点
;(2)点![]() 的坐标是
的坐标是![]() .
.
【解析】
(1)当![]() 时,解一元二次方程
时,解一元二次方程![]() ,得到方程的解,即可得到A、B的坐标;
,得到方程的解,即可得到A、B的坐标;
(2)先求出点C坐标,然后得到OB=OC,则![]() ,从而得到
,从而得到![]() ;根据
;根据![]() ,对点N进行分析,可分为①当点N在点C的右侧时,②当点N在点C的左侧时两类进行讨论分析,从而通过计算,得到点N的坐标.
,对点N进行分析,可分为①当点N在点C的右侧时,②当点N在点C的左侧时两类进行讨论分析,从而通过计算,得到点N的坐标.
解:(1)当![]() 时,
时,![]() ,
,
解得:![]() ,
,
∵点![]() 在点
在点![]() 的左侧,
的左侧,
∴点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ;
;
(2)连接![]() ,在
,在![]() 中,令
中,令![]() ,则
,则![]() .
.
即![]() 的坐标是
的坐标是![]() ,
,![]() .
.
∵点![]() 的坐标是
的坐标是![]() ,
,
∴![]() ,
,
∴![]() ,则
,则![]() 是等腰直角三角形.
是等腰直角三角形.
∴![]() .
.
过点![]() 作
作![]() 轴,垂足是
轴,垂足是![]() .
.

∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
设点![]() 的坐标是
的坐标是![]() ,当点
,当点![]() 在点
在点![]() 右侧时,
右侧时,
∴![]() ,
,
∴![]() ,
,
解得:![]() (舍去)或
(舍去)或![]()
∴点![]() 的坐标是
的坐标是![]() ;
;
当点![]() 在点
在点![]() 左侧时,
左侧时,
∴![]() ,
,
∴![]() ,
,
解得:![]() (舍去)或
(舍去)或![]() (舍去)
(舍去)
综上,点![]() 的坐标是
的坐标是![]() .
.


科目:初中数学 来源: 题型:
【题目】对于某一函数给出如下定义:对于任意实数![]() ,当自变量
,当自变量![]() 时,函数
时,函数![]() 关于
关于![]() 的函数图象为
的函数图象为![]() ,将
,将![]() 沿直线
沿直线![]() 翻折后得到的函数图象为
翻折后得到的函数图象为![]() ,函数
,函数![]() 的图象由
的图象由![]() 和
和![]() 两部分共同组成,则函数
两部分共同组成,则函数![]() 为原函数的“对折函数”,如函数
为原函数的“对折函数”,如函数![]() (
(![]() )的对折函数为
)的对折函数为![]() .
.
(1)求函数![]() (
(![]() )的对折函数;
)的对折函数;
(2)若点![]() 在函数
在函数![]() (
(![]() )的对折函数的图象上,求
)的对折函数的图象上,求![]() 的值;
的值;
(3)当函数![]() (
(![]() )的对折函数与
)的对折函数与![]() 轴有不同的交点个数时,直接写出
轴有不同的交点个数时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,点A的坐标为(0,1),取一点B(b,0),连接AB,作线段AB的垂直平分线![]() ,过点B作X轴的垂线
,过点B作X轴的垂线![]() ,记
,记![]() ,
,![]() 的交点为P。
的交点为P。
(1)当b=3时,在图1中补全图形(尺规作图,不写作法,保留作图痕迹)。
(2)小慧多次取不同数值b,得出相应的点P,并把这些点用平滑的曲线连接起来,发现:这些点P竟然在一条曲线L上。
①设点P的坐标为(x,y),试求y与x之间的关系式,并指出曲线L是哪种曲线。
②设点P到x轴,y轴的距离分别为![]() ,
,![]() ,求
,求![]() +
+![]() 的范围。当
的范围。当![]() +
+![]() =8时,求点P的坐标。
=8时,求点P的坐标。
③将曲线在直线y=2下方的部分沿直线y=2向上翻折,得到一条“W”形状的新曲线,若直线y=kx+3与这条“W”形状的新曲线有4个交点,直接写出k的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》“勾股”一章记载:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”译文:已知长方形门的高比宽多6尺8寸,门的对角线长1丈,那么门的高和宽各是多少?(1丈=10尺,1尺=10寸)设长方形门的宽![]() 尺,可列方程为_______.
尺,可列方程为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
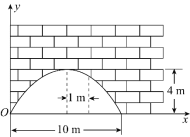
【题目】有一个抛物线形的拱形桥洞,桥面离水面的距离为5.6米,桥洞离水面的最大高度为![]() ,跨度为
,跨度为![]() ,如图所示,把它的图形放在直角坐标系中.
,如图所示,把它的图形放在直角坐标系中.
(1)求这条抛物线所对应的函数关系式.
(2)如图,在对称轴右边![]() 处,桥洞离桥面的高是多少?
处,桥洞离桥面的高是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-2x-2n=0有两个不相等的实数根,若n<5,且方程的两个实数根都是整数,则n的值为( )
A. n=2
B. n=0或n=1.5或n=4
C. n=4
D. n=0或n=1.5或n=2
查看答案和解析>>
科目:初中数学 来源: 题型:
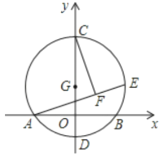
【题目】如图,以![]() 为圆心,半径为2的圆与
为圆心,半径为2的圆与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() ,
,![]() 两点,点
两点,点![]() 为圆
为圆![]() 上一动点,
上一动点,![]() 于
于![]() ,当点
,当点![]() 在圆
在圆![]() 的运动过程中,线段
的运动过程中,线段![]() 的长度的最小值为__________.
的长度的最小值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则S△CDF:S四边形ABFE等于( )
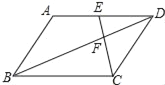
A. 1:3 B. 2:5 C. 3:5 D. 4:9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com