练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知：如下图，在等腰三角形ABC的两腰AB、AC上分别取点E、F，使AE＝CF，已知BC＝2，求证：EF≥1．

    答案：
    解析：

    　　分析：此题看似简单，却不易下手，若将图形补成以BC为一边且过点A的矩形，可使证明变得有的放矢．

    　　简评：巧把等腰三角形补成矩形，题目的条件变得整体化，给解题带来了方便．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：新课标3维同步训练与评价·数学·九年级·上 题型：047

    　　已知：如下图，在△ABC中D、E分别是AC、AB上的点，BD、CE交于O．

    　　给出下列四个条件①∠EBO＝∠DCO　②∠BEO＝∠CDO　③BE＝CD　④OB＝OC．

    　　(1)上述四个条件中，哪两个条件可以判别△ABC是等腰三角形(用序号写出所有情形)？

    　　(2)选择(1)中的一种情形，证明△ABC是等腰三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：044

    ．阅读材料：

    如图在四边形ABCD中，对角线AC⊥BD，垂足为P.


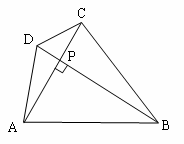
    求证：S四边形ABCD=

    证明：AC⊥BD→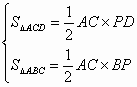

    ∴S四边形ABCD=S△ACD+S△ACB=

    =

    解答问题：

    　　(1）上述证明得到的性质可叙述为___________________________.

    　　(2）已知：如下图，等腰梯形ABCD中，AD∥BC，对角线AC⊥BD且相交于点P，BD=10cm，利用上述的性质求梯形的面积.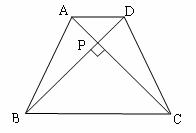

    查看答案和解析>>

    科目：初中数学 来源：2009年重庆市中考数学试卷 题型：044

    已知：如下图，在平面直角坐标系xOy中，矩形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA＝2，OC＝3．过原点O作∠AOC的平分线交AB于点D，连接DC，过点D作DE⊥DC，交OA于点E．

    (1)求过点E、D、C的抛物线的解析式；

    (2)将∠EDC绕点D按顺时针方向旋转后，角的一边与y轴的正半轴交于点F，另一边与线段OC交于点G．如果DF与(1)中的抛物线交于另一点M，点M的横坐标为，那么EF＝2GO是否成立？若成立，请给予证明；若不成立，请说明理由；

    (3)对于(2)中的点G，在位于第一象限内的该抛物线上是否存在点Q，使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形？若存在，请求出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：湖南省郴州市2011年中考数学试题 题型：059

    已知：如下图，等腰梯形ABCD的边BC在x轴上，点A在y轴的正方向上，A(0，6)，D(4，6)，且AB＝．

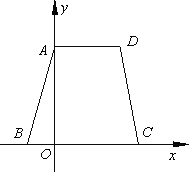
    (1)求点B的坐标；

    (2)求经过A、B、D三点的抛物线的解析式；

    (3)在(2)中所求的抛物线上是否存在一点P，使得？若存在，请求出该点坐标，若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案