
如图,已知直线 与反比例函数
与反比例函数 的图象相交于点A(-1,a),并且与x轴相交于点B.
的图象相交于点A(-1,a),并且与x轴相交于点B.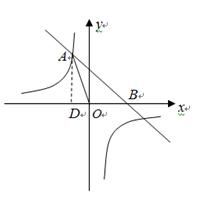
(1)求a的值;
(2)求反比例函数的表达式;
(3)求△AOB的面积.
(1)a=3;(2)求反比例函数的表达式 ;(3)△AOB的面积=3.
;(3)△AOB的面积=3.
解析试题分析:(1)直接利用待定系数法把A(﹣2,a)代入函数关系式y=﹣x+4中即可求出a的值;
(2)由(1)得到A点坐标后,设出反比例函数关系式,再把A点坐标代入反比例函数关系式,即可得到答案;
(3)根据题意画出图象,过A点作AD⊥x轴于D,根据A的坐标求出AD的长,再根据B点坐标求出OB的长,根据三角形面积公式即可算出△AOB的面积.
解:(1)将A(-1,a)代入y=-x+4中,
得:a=-(-1)+2 所以a=3
(2)由(1)得:A(-1,3)
将A(-1,3)代入 中,得到
中,得到
即k=-3
所以反比例函数的表达式为:
(3)过A点作AD⊥x轴于D
因为A(-1,3)所以AD=3
在直线y=-x+2中,令y=0,得x=2
所以B(2,0)即OB=2
所以△AOB的面积S= ×OB×AD=
×OB×AD= ×2×3=3
×2×3=3
考点:反比例函数与一次函数的交点问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
两个反比例函数 ,
, 在第一象限内的图像如图所示,点
在第一象限内的图像如图所示,点 ,
, ,
, ,…,
,…, 在函数
在函数 的图像上,它们的横坐标分别是
的图像上,它们的横坐标分别是 ,
, ,
, ,…,
,…, ,纵坐标分别是1,3,5,…,共2013个连续奇数,过点
,纵坐标分别是1,3,5,…,共2013个连续奇数,过点 ,
, ,
, ,…,
,…, 分别作y轴的平行线,与函数
分别作y轴的平行线,与函数 的图像交点依次是
的图像交点依次是 (
( ,
, ),
), (
( ,
,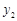 ),
),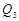 (
( ,
, ),…,
),…, (
( ,
, ),则
),则 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3).反比例函数 的函数图象经过点D,点P是一次函数y=kx+3-3k(k≠0)的图象与该反比例函数图象的一个公共点.
的函数图象经过点D,点P是一次函数y=kx+3-3k(k≠0)的图象与该反比例函数图象的一个公共点.
(1)求反比例函数的解析式;
(2)通过计算,说明一次函数y=kx+3-3k(k≠0)的图象一定过点C;
(3)对于一次函数y=kx+3-3k(k≠0),当y随x的增大而增大时,确定点P的横坐标的取值范围(不必写出过程).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,矩形OABC的顶点A、C分别在x轴和y轴上,点 的坐标为(2,3).双曲线
的坐标为(2,3).双曲线 的图像经过BC的中点D,且与AB交于点E,连接DE.
的图像经过BC的中点D,且与AB交于点E,连接DE.
(1)求k的值及点E的坐标;
(2)若点F是边上一点,且ΔFCB∽ΔDBE,求直线FB的解析式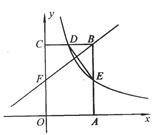
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知反比例函数y= (k为常数,k≠1).
(k为常数,k≠1).
(1)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;
(2)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;
(3)若其图象的一支位于第二象限,在这一支上任取两点 A(x1,y1)、B(x2,y2),当y1>y2时,试比较x1与x2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知反比例函数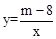 (m为常数)的图象经过点A(-1,6).
(m为常数)的图象经过点A(-1,6).
(1)求m的值;
(2)如图,过点A作直线AC与函数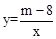 的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知一次函数 的图象与反比例函数
的图象与反比例函数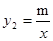 的图象的两个交点是A(-2,-4),C(4,n),与y轴交于点B,与x轴交于点D.
的图象的两个交点是A(-2,-4),C(4,n),与y轴交于点B,与x轴交于点D.
(1)求反比例函数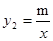 和一次函数
和一次函数 的解析式;
的解析式;
(2)连结OA,OC,求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
定义:已知反比例函数 与
与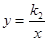 ,如果存在函数
,如果存在函数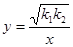 (
(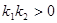 )则称函数
)则称函数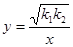 为这两个函数的中和函数.
为这两个函数的中和函数.
(1)试写出一对函数,使得它的中和函数为 ,并且其中一个函数满足:当
,并且其中一个函数满足:当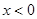 时,
时, 随
随 的增大而增大.
的增大而增大.
(2) 函数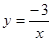 和
和 的中和函数
的中和函数 的图象和函数
的图象和函数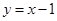 的图象相交于两点,试求当
的图象相交于两点,试求当 的函数值大于
的函数值大于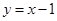 的函数值时
的函数值时 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com