
 如图,在⊙O中,AB是⊙O的直径,AC是⊙O的弦,过点C作⊙O的切线交BA的延长线于点P,连接BC.
如图,在⊙O中,AB是⊙O的直径,AC是⊙O的弦,过点C作⊙O的切线交BA的延长线于点P,连接BC.分析 (1)如图1中,连接OC.只要证明∠PCA+∠ACO=90°,∠B+∠OCA=90°,即可.
(2)①如图2中,当点Q在AB下方,$\widehat{AQ}$=$\widehat{BQ}$时,四边形AQBC的面积最大,此时t=$\frac{\frac{1}{4}×12π}{π}$=3s.
②如图3中,当$\widehat{AC}$=$\widehat{BQ}$时,四边形AQBC是矩形,连接CQ与AB交于点O.求出弧AQ的长即可解决问题.
解答 (1)证明:如图1中,连接OC.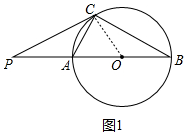
∵PC是切线,OC是半径,
∴OC⊥PC,
∴∠PCO=90°
∴∠PCA+∠ACO=90°,
∵AB是直径,
∴∠ACB=90°,
∴∠B+∠CAB=90°,
∵OC=OA,
∴∠OAC=∠OCA,
∴∠B+∠OCA=90°,
∴∠PCA=∠B.
(2)①如图2中,当点Q在AB下方,$\widehat{AQ}$=$\widehat{BQ}$时,四边形AQBC的面积最大,此时t=$\frac{\frac{1}{4}×12π}{π}$=3s.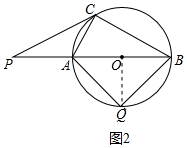
故答案为3s.
②如图3中,当$\widehat{AC}$=$\widehat{BQ}$时,四边形AQBC是矩形,连接CQ与AB交于点O.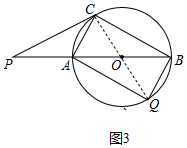
∵∠P=40°,∠PCO=90°,
∴∠POC=50°,
∴∠AOQ=130°,
∴弧AQ的长=$\frac{130π•6}{180}$=$\frac{13π}{3}$,
∴t=$\frac{\frac{13π}{3}}{π}$=$\frac{13}{3}$s.
故答案为$\frac{13}{3}$s.
点评 本题考查圆综合题、切线的性质、直径的性质、等角的余角相等、弧长公式等知识,解题的关键是灵活运用所学知识,学会寻找特殊点解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
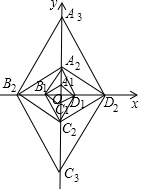 已知菱形A1B1C1D1的边长为2,∠A1B1C1=60°,对角线A1C1、B1D1相交于点O,以点O为坐标原点,分别以OB1,OA1所在直线为x轴、y轴建立如图所示的直角坐标系,以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1,再以A2C2为对角线作菱形A2B2C2D2∽菱形B1C2D1A2,再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2,…,按此规律继续作下去,在y轴的正半轴上得到点A1,A2,A3,…,An,则点A2017的坐标为(0,32016).
已知菱形A1B1C1D1的边长为2,∠A1B1C1=60°,对角线A1C1、B1D1相交于点O,以点O为坐标原点,分别以OB1,OA1所在直线为x轴、y轴建立如图所示的直角坐标系,以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1,再以A2C2为对角线作菱形A2B2C2D2∽菱形B1C2D1A2,再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2,…,按此规律继续作下去,在y轴的正半轴上得到点A1,A2,A3,…,An,则点A2017的坐标为(0,32016).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com