
分析 (1)根据判别式的意义得到△=4(a-1)2-4(a2-1)>0,然后解不等式得到a的范围;
(2)根据根与系数的关系得到m+n=2 (a-1)=2a-2,mn=a2-1,则由(m-1)(n-1)=10得到a2-1-(2a-2)+1=a2-2a+2=10,然后解关于a的方程即可得到满足条件的a的值.
解答 解:(1)由题意知△=4(a-1)2-4(a2-1)>0,
解得a<1;
(2)∵(m,0),(n,0)是抛物线y=x2-2(a-1)x+a2-1与x轴的两个不同交点,
∴m、n为方程x2-2(a-1)x+a2-1=0的两根,
∴m+n=2 (a-1)=2a-2,mn=a2-1,
∵(m-1)(n-1)=10,
即mn-(m+n)+1=10,
∴a2-1-(2a-2)+1=a2-2a+2=10,
解得a=-2或4(>1,舍去),
∴a的值是-2.
点评 本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.也考查了根与系数的关系.


科目:初中数学 来源: 题型:解答题
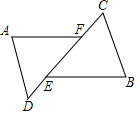 如图所示,△ADF和△BCE中,∠A=∠B,点D,E,F,C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF.请用其中两个关系式作为条件,另一个作为结论,写出的一个正确结论,并说明它正确的理由.
如图所示,△ADF和△BCE中,∠A=∠B,点D,E,F,C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF.请用其中两个关系式作为条件,另一个作为结论,写出的一个正确结论,并说明它正确的理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
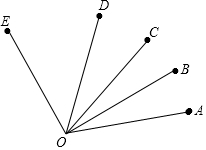 已知:如图,线段OA、OB、OC、OD、OE在同一平面内,且∠AOE=110°,∠AOB=20°.
已知:如图,线段OA、OB、OC、OD、OE在同一平面内,且∠AOE=110°,∠AOB=20°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 成绩 | 5 | 6 | 7 | 8 | 9 |
| 次数 | 1 | 2 | 4 | 2 | 1 |
| 成绩 | 3 | 4 | 6 | 7 | 8 | 9 | 10 |
| 次数 | 1 | 1 | 1 | 2 | 3 | 1 | 1 |
| 平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
| 甲 | 7 | 7 | 7 | 1.2 |
| 乙 | 7 | 7.5 | 8 | 4.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,∠AOB=90°,∠AOC为∠AOB外的一个锐角,且∠AOC=30°,射线OM平分∠BOC,ON平分∠AOC.
如图,∠AOB=90°,∠AOC为∠AOB外的一个锐角,且∠AOC=30°,射线OM平分∠BOC,ON平分∠AOC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3),△AOB绕点O逆时针旋转90°后得到△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3),△AOB绕点O逆时针旋转90°后得到△A1OB1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在⊙O中,AB是⊙O的直径,AC是⊙O的弦,过点C作⊙O的切线交BA的延长线于点P,连接BC.
如图,在⊙O中,AB是⊙O的直径,AC是⊙O的弦,过点C作⊙O的切线交BA的延长线于点P,连接BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com