
【题目】在平面直角坐标系xOy中,点A(t,0),B(t+2,0),C(n,1),若射线OC上存在点P,使得△ABP是以AB为腰的等腰三角形,就称点P为线段AB关于射线OC的等腰点.
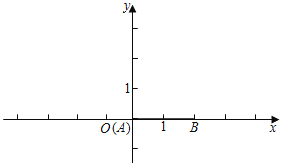
(1)如图,t=0,
①若n=0,则线段AB关于射线OC的等腰点的坐标是 ;
②若n<0,且线段AB关于射线OC的等腰点的纵坐标小于1,求n的取值范围;
(2)若n=![]() ,且射线OC上只存在一个线段AB关于射线OC的等腰点,则t的取值范围是 .
,且射线OC上只存在一个线段AB关于射线OC的等腰点,则t的取值范围是 .
【答案】(1)①(0,2) ②![]() (2)﹣4<t≤﹣2或t=0或
(2)﹣4<t≤﹣2或t=0或![]() ﹣2<t≤
﹣2<t≤![]()
【解析】
(1)①根据线段AB关于射线OC的等腰点的定义可知OP=AB=2,由此即可解决问题.
②如图2中,当OP=AB时,作PH⊥x轴于H.求出点P的横坐标,利用图象法即可解决问题.
(2)如图3﹣1中,作CH⊥y轴于H.分别以A,B为圆心,AB为半径作⊙A,⊙B.首先证明∠COH=30°,由射线OC上只存在一个线段AB关于射线OC的等腰点,推出射线OC与⊙A,⊙B只有一个交点,求出几种特殊位置t的值,利用数形结合的思想解决问题即可.
解:(1)①如图1中,由题意A(0,0),B(2,0),C(0,1),
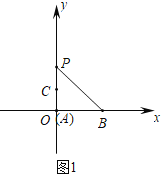
∵点P是线段AB关于射线OC的等腰点,
∴OP=AB=2,
∴P(0,2).
故答案为(0,2).
②如图2中,当OP=AB时,作PH⊥x轴于H.
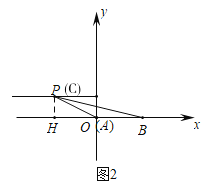
在Rt△POH中,∵PH=OC=1,OP=AB=2
∴OH=![]() =
=![]() ,
,
观察图象可知:若n<0,且线段AB关于射线OC的等腰点的纵坐标小于1时,n<﹣![]() .
.
(2)如图3﹣1中,作CH⊥y轴于H.分别以A,B为圆心,AB为半径作⊙A,⊙B.
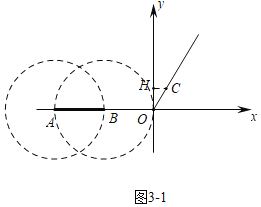
由题意C(![]() ,1),
,1),
∴CH=![]() ,OH=1,
,OH=1,
∴tan∠COH=![]() =
=![]() ,
,
∴∠COH=30°,
当⊙B经过原点时,B(﹣2,0),此时t=﹣4,
∵射线OC上只存在一个线段AB关于射线OC的等腰点,
∴射线OC与⊙A,⊙B只有一个交点,观察图象可知当﹣4<t≤﹣2时,满足条件,
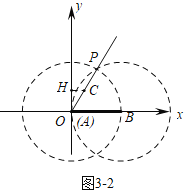
如图3﹣2中,当点A在原点时,∵∠POB=60°,此时两圆的交点P在射线OC上,满足条件,此时t=0,
如图3﹣3中,当⊙B与OC相切于P时,连接BP.
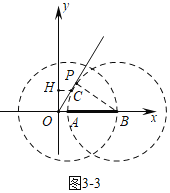
∴OC是⊙B的切线,
∴OP⊥BP,
∴∠OPB=90°,
∵BP=2,∠POB=60°,
∴OB=![]() =
=![]() ,此时t=
,此时t=![]() ﹣2,
﹣2,
如图3﹣4中,当⊙A与OC相切时,同法可得OA=![]() ,此时t=
,此时t=![]()
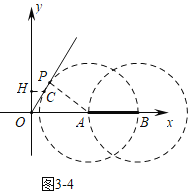
观察图形可知,满足条件的t的值为:![]() ﹣2<t≤
﹣2<t≤![]() ,
,
综上所述,满足条件t的值为﹣4<t≤﹣2或t=0或![]() ﹣2<t≤
﹣2<t≤![]() .
.
故答案为:﹣4<t≤﹣2或t=0或![]() ﹣2<t≤
﹣2<t≤![]() .
.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
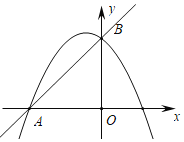
【题目】在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 、
、![]() .
.
(1)求![]() 、
、![]() 满足的关系式及
满足的关系式及![]() 的值.
的值.
(2)当![]() 时,若
时,若![]() 的函数值随
的函数值随![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
(3)如图,当![]() 时,在抛物线上是否存在点
时,在抛物线上是否存在点![]() ,使
,使![]() 的面积为1?若存在,请求出符合条件的所有点
的面积为1?若存在,请求出符合条件的所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() 是射线
是射线![]() 上一点,
上一点,![]() .动点
.动点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 水平向左作匀速运动,与此同时,动点
水平向左作匀速运动,与此同时,动点![]() 从点
从点![]() 出发,也以
出发,也以![]() 的速度沿
的速度沿![]() 竖直向上作匀速运动.连接
竖直向上作匀速运动.连接![]() ,交
,交![]() 于点
于点![]() .经过
.经过![]() 、
、![]() 、
、![]() 三点作圆,交
三点作圆,交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .设运动时间为
.设运动时间为![]() ,其中
,其中![]() .
.
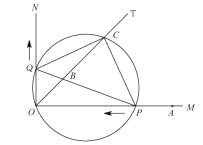
(1)求![]() 的值;
的值;
(2)是否存在实数![]() ,使得线段
,使得线段![]() 的长度最大?若存在,求出
的长度最大?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(3)求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
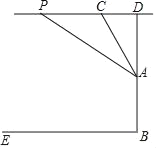
【题目】如图,滑翔运动员在空中测量某寺院标志性高塔“云端塔”的高度,空中的点P距水平地面BE的距离为200米,从点P观测塔顶A的俯角为33°,以相同高度继续向前飞行120米到达点C,在C处观测点A的俯角是60°,求这座塔AB的高度(结果精确到1米).(参考数据:sin33°≈0.54,cos33°≈0.84,tan33°≈0.65,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
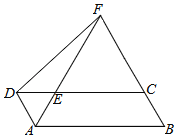
【题目】如图,在ABCD中,∠ABC=60°,∠BAD的平分线交CD于点E,交BC的延长线于点F,连接DF.
(1)求证:△ABF是等边三角形;
(2)若∠CDF=45°,CF=2,求AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
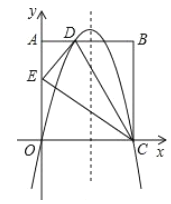
【题目】如图,在矩形![]() 中,点
中,点![]() . 沿直线
. 沿直线![]() 折叠矩形
折叠矩形![]() ,使点
,使点![]() 落在
落在![]() 边上,与点
边上,与点![]() 重合.分别以
重合.分别以![]() ,
,![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 轴建立平面直角坐标系,抛物线
轴建立平面直角坐标系,抛物线![]() 经过
经过![]() 两点.
两点.
(1)求![]() 及点
及点![]() 的坐标;
的坐标;
(2)一动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒
以每秒![]() 个单位长的速度向点
个单位长的速度向点![]() 运动, 同时动点
运动, 同时动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒
以每秒![]() 个单位长的速度向点
个单位长的速度向点![]() 运动, 当点
运动, 当点![]() 运动到点
运动到点![]() 时,两点同时停止运动.设运动时间为
时,两点同时停止运动.设运动时间为![]() 秒,当
秒,当![]() 为何值时,以
为何值时,以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
(3)点![]() 在抛物线对称轴上,点
在抛物线对称轴上,点![]() 在抛物线上,是否存在这样的点
在抛物线上,是否存在这样的点![]() 与点 N,使以
与点 N,使以![]() ,
,![]() ,
,![]() ,
, ![]() 为顶点的四边形是平行四边形?若存在,请直接写出点
为顶点的四边形是平行四边形?若存在,请直接写出点![]() 与点
与点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
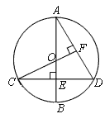
(1)证明:点E是OB的中点;
(2)若AB=8,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
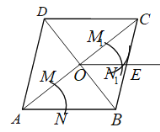
【题目】如图,菱形![]() 的对角线
的对角线![]() 相交于点
相交于点![]() 按下列步骤作图:①以点
按下列步骤作图:①以点![]() 为圆心,任意长为半径作弧,分别交
为圆心,任意长为半径作弧,分别交![]() 于点
于点![]() ;②以点
;②以点![]() 为圆心,
为圆心,![]() 长为半径作弧,交
长为半径作弧,交![]() 于点
于点![]() ;③点
;③点![]() 为圆心,
为圆心,![]() 以长为半径作弧,在
以长为半径作弧,在![]() 内部交②中所作的圆弧于点
内部交②中所作的圆弧于点![]() ;④过点
;④过点![]() 作射线
作射线![]() 交
交![]() 于点
于点![]() .
.![]() ,四边形
,四边形![]() 的面积为( )
的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快车和慢车分别从![]() 市和
市和![]() 市两地同时出发,匀速行驶,先相向而行,慢车到达
市两地同时出发,匀速行驶,先相向而行,慢车到达![]() 市后停止行驶,快车到达
市后停止行驶,快车到达![]() 市后,立即按原路原速度返回
市后,立即按原路原速度返回![]() 市(调头时间忽略不计),结果与慢车同时到达
市(调头时间忽略不计),结果与慢车同时到达![]() 市.快、慢两车距
市.快、慢两车距![]() 市的路程
市的路程![]() 、
、![]() (单位:
(单位:![]() )与出发时间
)与出发时间![]() (单位:
(单位:![]() )之间的函数图像如图所示.
)之间的函数图像如图所示.
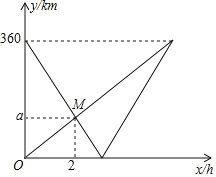
(1)![]() 市和
市和![]() 市之间的路程是________
市之间的路程是________![]() ,图中
,图中![]() ____________;
____________;
(2)请求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)快车与慢车迎面相遇以后,请直接写出经过多长时间两车相距![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com