
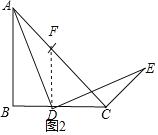
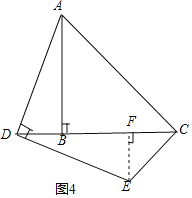
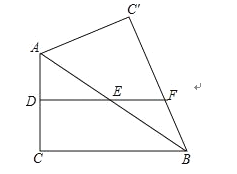
ΓΨΧβΡΩΓΩ‘ΎΓςABC÷–Θ§ABΘΫBCΘ§ΓœBΘΫ90ΓψΘ§ΒψDΈΣ÷±œΏBC…œΒΡ“ΜΗωΕ·Βψ(≤Μ”κBΓΔC÷ΊΚœ)Θ§Ν§ΫαADΘ§ΫΪœΏΕΈAD»ΤΒψDΑ¥Υ≥ ±’κΖΫœρ–ΐΉΣ90ΓψΘ§ ΙΒψA–ΐΉΣΒΫΒψEΘ§Ν§ΫαECΘ°
(1)»γΙϊΒψD‘ΎœΏΕΈBC…œ‘ΥΕ·Θ§»γΆΦ1ΘΚ
ΔΌ“άΧβ“β≤Ι»ΪΆΦ1ΘΜ
ΔΎ«σ÷ΛΘΚΓœBADΘΫΓœEDCΘΜ
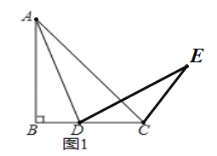
ΔέΆ®ΙΐΙέ≤λΓΔ Β―ιΘ§–ΓΟςΒΟ≥ωΫα¬έΘΚ‘ΎΒψD‘ΥΕ·ΒΡΙΐ≥Χ÷–Θ§Ήή”–ΓœDCEΘΫ135ΓψΘ§Θ°
–ΓΟς”κΆ§―ßΧ÷¬έΚσΘ§–Έ≥…ΝΥ÷ΛΟς’βΗωΫα¬έΒΡΦΗ÷÷œκΖ®ΘΚ
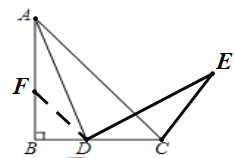
œκΖ®“ΜΘΚ‘ΎAB…œ»Γ“ΜΒψFΘ§ ΙΒΟBFΘΫBDΘ§“Σ÷ΛΓœDCEΘΫ135ΓψΘ§÷Μ–η÷ΛΓςADFΓ’ΓςDECΘ°
œκΖ®ΕΰΘΚ“‘ΒψDΈΣ‘≤–ΡΘ§DCΈΣΑκΨΕΜ≠ΜΓΫΜAC”ΎΒψFΘ§“Σ÷ΛΓœDCEΘΫ135ΓψΘ§÷Μ–η÷ΛΓςAFDΓ’ΓςDCEΘ°
œκΖ®»ΐΘΚΙΐΒψEΉςBCΥυ‘Ύ÷±œΏΒΡ¥Ι÷±œΏΕΈEFΘ§“Σ÷ΛΓœDCEΘΫ135ΓψΘ§÷Μ–η÷ΛEFΘΫCFΘ°
«κΡψ≤ΈΩΦ…œΟφΒΡœκΖ®Θ§÷ΛΟςΓœDCEΘΫ135Γψ
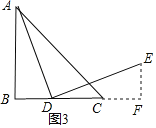
(2)»γΙϊΒψD‘ΎœΏΕΈCBΒΡ―”≥ΛœΏ…œ‘ΥΕ·Θ§άϊ”ΟΆΦ2Μ≠ΆΦΖ÷ΈωΘ§ΓœDCEΒΡΕ» ΐΜΙ «»ΖΕ®ΒΡ÷Β¬πΘΩ»γΙϊ «Θ§÷±Ϋ”–¥≥ωΓœDCEΒΡΕ» ΐΘΜ»γΙϊ≤Μ «Θ§ΥΒΟςάμ”…Θ°
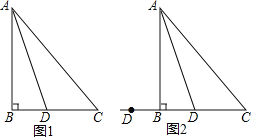
ΓΨ¥πΑΗΓΩ(1)ΔΌΦϊΫβΈωΘΜΔΎ÷ΛΟςΦϊΫβΈωΘΜΔέ÷ΛΟςΦϊΫβΈωΘΜ(2)ΓœDCEΘΫ45Γψ.
ΓΨΫβΈωΓΩ
(1)ΔΌΗυΨίΧβ“βΉς≥ωΆΦ–ΈΦ¥Ω…ΘΜΔΎΗυΨί”ύΫ«ΒΡ–‘÷ ΒΟΒΫΫα¬έΘΜΔέ÷ΛΖ®1ΘΚ‘ΎAB…œ»ΓΒψFΘ§ ΙΒΟBFΘΫBDΘ§Ν§Ϋ”DFΘ§ΗυΨίΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫΓœBFDΘΫ45ΓψΘ§ΗυΨί»ΪΒ»»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫΓœDCEΘΫΓœAFDΘΫ135ΓψΘΜ÷ΛΖ®2ΘΚ“‘DΈΣ‘≤–ΡΘ§DCΈΣΑκΨΕΉςΜΓΫΜAC”ΎΒψFΘ§Ν§Ϋ”DFΘ§ΗυΨί»ΪΒ»»ΐΫ«–ΈΒΡ–‘÷ Φ¥Ω…ΒΟΒΫΫα¬έΘΜ÷ΛΖ®3ΘΚΙΐΒψEΉςEFΓΆBCΫΜBCΒΡ―”≥ΛœΏ”ΎΒψFΘ§ΗυΨί»ΪΒ»»ΐΫ«–ΈΒΡ–‘÷ Φ¥Ω…ΒΟΒΫΫα¬έΘΜ
(2)ΙΐEΉςEFΓΆDC”ΎFΘ§ΗυΨί»ΪΒ»»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫDBΘΫEFΘ§ABΘΫDFΘΫBCΘ§ΗυΨίœΏΕΈΒΡΚΆ≤νΒΟΒΫFCΘΫEFΘ§”Ύ «ΒΟΒΫΫα¬έΘ°
ΫβΘΚ(1)ΔΌ»γΆΦΔΌΥυ ΨΘΜ
ΔΎ÷ΛΟςΘΚΓΏΓœBΘΫ90ΓψΘ§
ΓύΓœBAD+ΓœBDAΘΫ90ΓψΘ§
ΓΏΓœADEΘΫ90ΓψΘ§ΒψD‘ΎœΏΕΈBC…œΘ§
ΓύΓœBAD+ΓœEDCΘΫ90ΓψΘ§
ΓύΓœBADΘΫΓœEDCΘΜ
ΔΎ÷ΛΖ®1ΘΚ»γΆΦΘ§‘ΎAB…œ»ΓΒψFΘ§ ΙΒΟBFΘΫBDΘ§Ν§Ϋ”DFΘ§
ΓΏBFΘΫBDΘ§ΓœBΘΫ90ΓψΘ§
ΓύΓœBFDΘΫ45ΓψΘ§
ΓύΓœAFDΘΫ135ΓψΘ§
ΓΏBAΘΫBCΘ§
ΓύAFΘΫCDΘ§
‘ΎΓςADFΚΆΓςDEC÷–Θ§
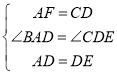
ΓύΓςADFΓ’ΓςDECΘ§
ΓύΓœDCEΘΫΓœAFDΘΫ135ΓψΘΜ
÷ΛΖ®2ΘΚ“‘DΈΣ‘≤–ΡΘ§DCΈΣΑκΨΕΉςΜΓΫΜAC”ΎΒψFΘ§Ν§Ϋ”DFΘ§
ΓύDCΘΫDFΘ§ΓœDFCΘΫΓœDCFΘ§
ΓΏΓœBΘΫ90ΓψΘ§ABΘΫBCΘ§
ΓύΓœACBΘΫ45ΓψΘ§ΓœDFCΘΫ45ΓψΘ§
ΓύΓœDFCΘΫ90ΓψΘ§ΓœAFDΘΫ135ΓψΘ§
ΓΏΓœADEΘΫΓœFDCΘΫ90ΓψΘ§
ΓύΓœADFΘΫΓœEDCΘ§
‘ΎΓςADFΓ’ΓςCDE÷–Θ§ Θ§
Θ§
ΓύΓςADFΓ’ΓςCDEΘ§
ΓύΓœAFDΘΫΓœDCEΘΫ135ΓψΘΜ
÷ΛΖ®3ΘΚΙΐΒψEΉςEFΓΆBCΫΜBCΒΡ―”≥ΛœΏ”ΎΒψFΘ§
ΓύΓœEFDΘΫ90ΓψΘ§
ΓΏΓœBΘΫ90ΓψΘ§
ΓύΓœEFDΘΫΓœBΘ§
‘ΎΓςABDΚΆΓςDFE÷–Θ§ Θ§
Θ§
ΓύΓςABDΓ’ΓςDFEΘ§
ΓύABΘΫDFΘ§BDΘΫEFΘ§
ΓΏABΘΫBCΘ§
ΓύBCΘΫDFΘ§BC©¹DCΘΫDF©¹DCΘ§
Φ¥BDΘΫCFΘ§
ΓύEFΘΫCFΘ§
ΓΏΓœEFCΘΫ90ΓψΘ§
ΓύΓœECFΘΫ45ΓψΘ§ΓœDCEΘΫ135ΓψΘΜ
(2)ΫβΘΚΓœDCEΘΫ45ΓψΘ§
άμ”…ΘΚΙΐEΉςEFΓΆDC”ΎFΘ§
ΓΏΓœABDΘΫ90ΓψΘ§
ΓύΓœEDFΘΫΓœDABΘΫ90Γψ©¹ΓœADBΘ§
‘ΎΓςABDΚΆΓςDFE÷–Θ§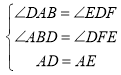 Θ§
Θ§
ΓύΓςABDΓ’ΓςDFEΘ§
ΓύDBΘΫEFΘ§ABΘΫDFΘΫBCΘ§
ΓύBC©¹BFΘΫDF©¹BFΘ§
Φ¥FCΘΫDBΘ§
ΓύFCΘΫEFΘ§
ΓύΓœDCEΘΫ45ΓψΘ°


 ΫΧ≤Ρ»ΪΫβΉ÷¥ ΨδΤΣœΒΝ–¥πΑΗ
ΫΧ≤Ρ»ΪΫβΉ÷¥ ΨδΤΣœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ¬Χ…Ϊ≥ω–– «Ε‘ΜΖΨ≥”ΑœλΉν–ΓΒΡ≥ω––ΖΫ ΫΘ§ΓΑΙ≤œμΒΞ≥ΒΓ±“―≥…ΈΣ±±Ψ©ΒΡ“ΜΒάωΠάωΒΡΖγΨΑœΏΘ°Ρ≥…γΜα ΒΦυΜνΕ·–Γ
ΉιΈΣΝΥΝΥΫβΓΑΙ≤œμΒΞ≥ΒΓ±ΒΡ Ι”Ο«ιΩωΘ§Ε‘±Ψ–ΘΫΧ Π‘Ύ3‘¬6»’÷Ν3‘¬10»’ Ι”ΟΒΞ≥ΒΒΡ«ιΩωΫχ––ΝΥΈ ΨμΒς≤ιΘ§
“‘œ¬ «ΗυΨίΒς≤ιΫαΙϊΜφ÷ΤΒΡΆ≥ΦΤΆΦΒΡ“Μ≤ΩΖ÷ΘΚ
«κΗυΨί“‘…œ–≈œΔΫβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©3‘¬7»’ Ι”ΟΓΑΙ≤œμΒΞ≥ΒΓ±ΒΡΫΧ Π»Υ ΐΈΣ»ΥΘ§≤Δ«κ≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘΜ
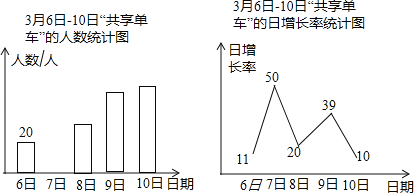
Θ®2Θ©≤ΜΆ§ΤΖ≈ΤΒΡΓΑΙ≤œμΒΞ≥ΒΓ±ΗςΨΏΧΊ…ΪΘ§…γΜα ΒΦυΜνΕ·–ΓΉι’κΕ‘”–Ιΐ Ι”ΟΓΑΙ≤œμΒΞ≥ΒΓ±Ψ≠άζΒΡΫΧ ΠΉωΝΥΫχ“Μ≤ΫΒς≤ιΘ§ΟΩΈΜΫΧ ΠΕΦΑ¥“Σ«σ―Γ‘ώΝΥ“Μ÷÷Ή‘ΦΚœ≤ΜΕΒΡΓΑΙ≤œμΒΞ≥ΒΓ±Θ§Ά≥ΦΤΫαΙϊ»γΆΦΘ§Τδ÷–œ≤ΜΕ![]() ΒΡΫΧ Π”–36»ΥΘ§«σœ≤ΜΕ
ΒΡΫΧ Π”–36»ΥΘ§«σœ≤ΜΕ![]() ΒΡΫΧ ΠΒΡ»Υ ΐΘ°
ΒΡΫΧ ΠΒΡ»Υ ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ÷±Ϋ«»ΐΫ«–Έ![]() ÷–Θ§
÷–Θ§![]() Θ§Βψ
Θ§Βψ![]() Θ§
Θ§![]() Ζ÷±πΈΣ
Ζ÷±πΈΣ![]() Θ§
Θ§![]() ΒΡ÷–ΒψΘ§ΫΪ
ΒΡ÷–ΒψΘ§ΫΪ![]() ―Ί
―Ί![]() Ζ≠’έΘ§ΒΟΒΫ
Ζ≠’έΘ§ΒΟΒΫ![]() Θ§
Θ§![]() ΒΡ―”≥ΛœΏΫΜ
ΒΡ―”≥ΛœΏΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ°
Θ°
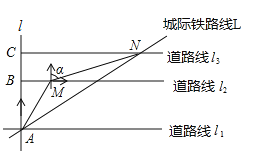
Θ®1Θ©≈–Εœ![]() ΒΡ–ΈΉ¥ΈΣ ΘΜ
ΒΡ–ΈΉ¥ΈΣ ΘΜ
Θ®2Θ©Β±![]() ±Θ§«σ÷ΛΥΡ±Ώ–Έ
±Θ§«σ÷ΛΥΡ±Ώ–Έ![]() ΈΣ’ΐΖΫ–ΈΘΜ
ΈΣ’ΐΖΫ–ΈΘΜ
Θ®3Θ©»τ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§Β±
Θ§Β±![]() ±Θ§÷±Ϋ”–¥≥ω
±Θ§÷±Ϋ”–¥≥ω![]() ΒΡ≥ΛΘ°
ΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΈΣΡ≥«χ”ρ≤ΩΖ÷ΫΜΆ®œΏ¬ΖΆΦΘ§Τδ÷–÷±œΏ![]() Θ§÷±œΏ
Θ§÷±œΏ![]() ”κ÷±œΏ
”κ÷±œΏ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΕΦ¥Ι÷±Θ§¥ΙΉψΖ÷±πΒψ
ΕΦ¥Ι÷±Θ§¥ΙΉψΖ÷±πΒψ![]() ΓΔΒψ
ΓΔΒψ![]() ΚΆΒψ
ΚΆΒψ![]() Θ§Θ®ΗΏΥΌ¬Ζ”“≤ύ±Ώ‘ΒΘ©Θ§
Θ§Θ®ΗΏΥΌ¬Ζ”“≤ύ±Ώ‘ΒΘ©Θ§![]() …œΒΡΒψ
…œΒΡΒψ![]() ΈΜ”ΎΒψ
ΈΜ”ΎΒψ![]() ΒΡ±±ΤΪΕΪ
ΒΡ±±ΤΪΕΪ![]() ΖΫœρ…œΘ§«“
ΖΫœρ…œΘ§«“![]() «ßΟΉΘ§
«ßΟΉΘ§![]() …œΒΡΒψ
…œΒΡΒψ![]() ΈΜ”ΎΒψ
ΈΜ”ΎΒψ![]() ΒΡ±±ΤΪΕΪ
ΒΡ±±ΤΪΕΪ![]() ΖΫœρ…œΘ§«“
ΖΫœρ…œΘ§«“![]() Θ§
Θ§![]() «ßΟΉΘ°Βψ
«ßΟΉΘ°Βψ![]() ΚΆΒψ
ΚΆΒψ![]() «≥«Φ œΏ
«≥«Φ œΏ![]() …œΒΡΝΫΗωœύΝΎΒΡ’ΨΒψΘ°
…œΒΡΝΫΗωœύΝΎΒΡ’ΨΒψΘ°
Θ®1Θ©«σ![]() ΚΆ
ΚΆ![]() ÷°ΦδΒΡΨύάκΘΜ
÷°ΦδΒΡΨύάκΘΜ
Θ®2Θ©»τ≥«Φ Μπ≥ΒΤΫΨυ ±ΥΌΈΣ![]() «ßΟΉ/–ΓÖΦΘ§«σ –Οώ–Γ«Ω≥ΥΉχ≥«Φ Μπ≥Β¥”’ΨΒψ
«ßΟΉ/–ΓÖΦΘ§«σ –Οώ–Γ«Ω≥ΥΉχ≥«Φ Μπ≥Β¥”’ΨΒψ![]() ΒΫ’ΨΒψ
ΒΫ’ΨΒψ![]() –η“ΣΕύ…Ό–Γ ±ΘΩΘ®ΫαΙϊ”ΟΖ÷ ΐ±μ ΨΘ©
–η“ΣΕύ…Ό–Γ ±ΘΩΘ®ΫαΙϊ”ΟΖ÷ ΐ±μ ΨΘ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
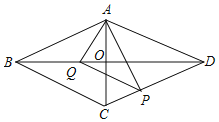
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ»γΆΦΘ§ΒψAΘ§BΘ§C»ΐΒψ‘ΎΓ―O…œΘ§AEΤΫΖ÷ΓœBACΘ§ΫΜΓ―O”ΎΒψEΘ§ΫΜBC”ΎΒψDΘ§ΙΐΒψEΉς÷±œΏlΓΈBCΘ§Ν§ΫαBEΘ°
(1)«σ÷ΛΘΚ÷±œΏl «Γ―OΒΡ«–œΏΘΜ
(2)»γΙϊDEΘΫaΘ§AEΘΫbΘ§–¥≥ω«σBEΒΡ≥ΛΒΡΥΦ¬ΖΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
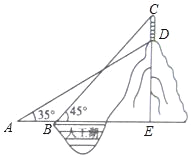
ΓΨΧβΡΩΓΩΡ≥ΙΪ‘ΑΒΡ»ΥΙΛΚΰ±Ώ…œ”–“ΜΉυΦΌ…ΫΘ§ΦΌ…ΫΕΞ…œ”–“Μ ζΤπΒΡΫ®÷ΰΈοCDΘ§ΗΏΈΣ10ΟΉΘ§ ΐ―ß–ΓΉιΈΣΝΥ≤βΝΩΦΌ…ΫΒΡΗΏΕ»DEΘ§‘ΎΙΪ‘Α’“ΝΥ“ΜΥ°ΤΫΒΊΟφΘ§‘ΎA¥Π≤βΒΟΫ®÷ΰΈοΒψDΘ®Φ¥…ΫΕΞΘ©ΒΡ―ωΫ«ΈΣ35ΓψΘ§―ΊΥ°ΤΫΖΫœρ«ΑΫχ20ΟΉΒΫ¥οBΒψΘ§≤βΒΟΫ®÷ΰΈοΕΞ≤ΩCΒψΒΡ―ωΫ«ΈΣ45ΓψΘ§«σΦΌ…ΫΒΡΗΏΕ»DEΘ°Θ®ΫαΙϊΨΪ»ΖΒΫ1ΟΉΘ§≤ΈΩΦ ΐΨίΘΚsin35ΓψΓ÷![]() Θ§cos35ΓψΓ÷
Θ§cos35ΓψΓ÷![]() Θ§tan35ΓψΓ÷
Θ§tan35ΓψΓ÷![]() Θ©
Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΝβ–Έ![]() ÷–Θ§Ε‘Ϋ«œΏ
÷–Θ§Ε‘Ϋ«œΏ![]() Θ§
Θ§![]() Θ§Ε·Βψ
Θ§Ε·Βψ![]() ΓΔ
ΓΔ![]() Ζ÷±π¥”Βψ
Ζ÷±π¥”Βψ![]() ΓΔ
ΓΔ![]() Ά§ ±≥ωΖΔΘ§‘ΥΕ·ΥΌΕ»ΕΦ «
Ά§ ±≥ωΖΔΘ§‘ΥΕ·ΥΌΕ»ΕΦ «![]() Θ§Βψ
Θ§Βψ![]() ”…
”…![]() œρ
œρ![]() ‘ΥΕ·ΘΜΒψ
‘ΥΕ·ΘΜΒψ![]() ”…
”…![]() œρ
œρ![]() ‘ΥΕ·Θ§Β±
‘ΥΕ·Θ§Β±![]() ΒΫ¥ο
ΒΫ¥ο![]() ±Θ§
±Θ§![]() ΓΔ
ΓΔ![]() ΝΫΒψ‘ΥΕ·ΆΘ÷ΙΘ§…η ±ΦδΈΣ
ΝΫΒψ‘ΥΕ·ΆΘ÷ΙΘ§…η ±ΦδΈΣ![]() Οκ(
Οκ(![]() )Θ°Ν§Ϋ”
)Θ°Ν§Ϋ”![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ°
Θ°
(1)Β±![]() ΈΣΚΈ÷Β ±Θ§
ΈΣΚΈ÷Β ±Θ§![]() ΘΜ
ΘΜ
(2)…η![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() Θ§«κ–¥≥ω
Θ§«κ–¥≥ω![]() ”κ
”κ![]() ΒΡΚ· ΐΙΊœΒ ΫΘΜ
ΒΡΚ· ΐΙΊœΒ ΫΘΜ
(3)Β±![]() ΈΣΚΈ÷Β ±Θ§
ΈΣΚΈ÷Β ±Θ§![]() ΒΡΟφΜΐ «ΥΡ±Ώ–Έ
ΒΡΟφΜΐ «ΥΡ±Ώ–Έ![]() ΟφΜΐΒΡ
ΟφΜΐΒΡ![]() ΘΩ
ΘΩ
(4) «Ζώ¥φ‘Ύ![]() ÷ΒΘ§ ΙΒΟœΏΕΈ
÷ΒΘ§ ΙΒΟœΏΕΈ![]() Ψ≠Ιΐ
Ψ≠Ιΐ![]() ΒΡ÷–Βψ
ΒΡ÷–Βψ![]() ΘΩ»τ¥φ‘ΎΘ§«σ≥ω
ΘΩ»τ¥φ‘ΎΘ§«σ≥ω![]() ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§“―÷Σ÷±œΏl1ΘΚy=mx(mΓΌ0) ”κ÷±œΏl2ΘΚy=ax+b(aΓΌ0) œύΫΜ”ΎΒψ AΘ®1Θ§2Θ©Θ§÷±œΏl2”κ x÷αΫΜ”ΎΒψBΘ®3Θ§0Θ©Θ°
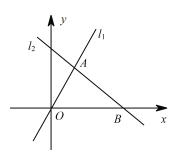
Θ®1Θ©Ζ÷±π«σ÷±œΏl1 ΚΆl2ΒΡ±μ¥ο ΫΘΜ
Θ®2Θ©ΙΐΕ·ΒψPΘ®0Θ§nΘ©«“ΤΫ––”Ύx÷αΒΡ÷±œΏ”κl1 Θ§l2ΒΡΫΜΒψΖ÷±πΈΣC Θ§DΘ§Β±Βψ C ΈΜ”ΎΒψ D ΉσΖΫ ±Θ§–¥≥ω nΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ”–’β―υ“ΜΗωΈ ΧβΘΚΧΫΨΩΚ· ΐ![]() ΒΡΆΦœσ”κ–‘÷ Θ°
ΒΡΆΦœσ”κ–‘÷ Θ°
–ΓΕΪΗυΨί―ßœΑΚ· ΐΒΡΨ≠―ιΘ§Ε‘Κ· ΐ![]() ΒΡΆΦœσ”κ–‘÷ Ϋχ––ΝΥΧΫΨΩΘ°
ΒΡΆΦœσ”κ–‘÷ Ϋχ––ΝΥΧΫΨΩΘ°
œ¬Οφ «–ΓΕΪΒΡΧΫΨΩΙΐ≥ΧΘ§«κ≤Ι≥δΆξ’ϊΘ§≤ΔΫβΨωœύΙΊΈ ΧβΘΚ
Θ®1Θ©Κ· ΐ![]() ΒΡΉ‘±δΝΩxΒΡ»Γ÷ΒΖΕΈß « ΘΜ
ΒΡΉ‘±δΝΩxΒΡ»Γ÷ΒΖΕΈß « ΘΜ
Θ®2Θ©œ¬±μ «y”κxΒΡΦΗΉιΕ‘”Π÷ΒΘ§«σmΒΡ÷ΒΘΜ
x | Γ≠ |
|
|
|
|
|
|
| 1 | 2 | 3 | 4 | Γ≠ |
y | Γ≠ |
|
|
|
|
|
|
|
|
|
| m | Γ≠ |
Θ®3Θ©»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§Οη≥ωΝΥ“‘…œ±μ÷–ΗςΕ‘Ε‘”Π÷ΒΈΣΉχ±ξΒΡΒψΘ°ΗυΨίΟη≥ωΒΡΒψΘ§Μ≠≥ωΗΟΚ· ΐΒΡΆΦœσΘΜ
Θ®4Θ©Ϋχ“Μ≤ΫΧΫΨΩΖΔœ÷Θ§ΗΟΚ· ΐΆΦœσ‘ΎΒΎΕΰœσœόΡΎΒΡΉνΒΆΒψΒΡΉχ±ξ «![]() Θ§ΫαΚœΚ· ΐΒΡΆΦœσΘ§–¥≥ωΗΟΚ· ΐΒΡΤδΥϋ–‘÷ Θ®“ΜΧθΦ¥Ω…Θ© Θ°
Θ§ΫαΚœΚ· ΐΒΡΆΦœσΘ§–¥≥ωΗΟΚ· ΐΒΡΤδΥϋ–‘÷ Θ®“ΜΧθΦ¥Ω…Θ© Θ°
Θ®5Θ©ΗυΨίΚ· ΐΆΦœσΙάΥψΖΫ≥Χ![]() ΒΡΗυΈΣ Θ°Θ®ΨΪ»ΖΒΫ0.1Θ©
ΒΡΗυΈΣ Θ°Θ®ΨΪ»ΖΒΫ0.1Θ©
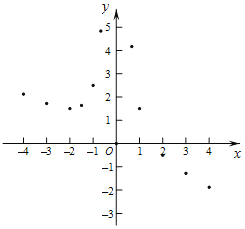
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com