
【题目】如图,在平面直角坐标系中,过点![]() 的直线
的直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,动点
,动点![]() 在线段
在线段![]() 和射线
和射线![]() 上运动.
上运动.
(1)求直线![]() 的解析式.
的解析式.
(2)求![]() 的面积.
的面积.
(3)是否存在点![]() ,使
,使![]() 的面积是
的面积是![]() 的面积的
的面积的![]() ?若存在求出此时点
?若存在求出此时点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
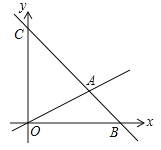
【答案】(1)y=-x+6;(2)12;(3)M1(2,1)或M2(2,4)或M3(-2,8).
【解析】
(1)利用待定系数法即可求得函数的解析式;
(2)求得C的坐标,即OC的长,利用三角形的面积公式即可求解;
(3)当△OMC的面积是△OAC的面积的![]() 时,根据面积公式即可求得M的横坐标,然后代入解析式即可求得M的坐标.
时,根据面积公式即可求得M的横坐标,然后代入解析式即可求得M的坐标.
解:(1)设直线AB的解析式是y=kx+b,
根据题意得![]() ,
,
解得:![]() ,
,
则直线的解析式是:y=-x+6;
(2)在y=-x+6中,令x=0,解得:y=6,
S△OAC=![]() ×6×4=12;
×6×4=12;
(3)设OA的解析式是y=mx,则4m=2,
解得:m=![]() ,
,
则直线的解析式是:y=![]() x,
x,
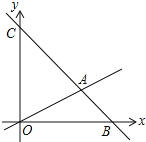
∵当△OMC的面积是△OAC的面积的![]() 时,
时,
又∵动点![]() 在线段
在线段![]() 和射线
和射线![]() 上运动
上运动
∴①当M的横坐标是![]() ×4=2,
×4=2,
在y=![]() x中,当x=2时,y=1,则M的坐标是(2,1);
x中,当x=2时,y=1,则M的坐标是(2,1);
在y=-x+6中,x=2则y=4,则M的坐标是(2,4).
则M的坐标是:M1(2,1)或M2(2,4).
②当M的横坐标是:-2,
在y=-x+6中,当x=-2时,y=8,则M的坐标是(-2,8);
综上所述:M的坐标是:M1(2,1)或M2(2,4)或M3(-2,8).


 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D是边AC上一点,BC=BD=AD,则∠A的大小是( ).

A. 36° B. 54° C. 72° D. 30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量平地上一块不规则区域(图中的阴影部分)的面积,画一个边长为4m的正方形,使不规则区域落在正方形内.现向正方形内随机投掷小球(假设小球落在正方形内每一点都是等可能的),经过大量重复投掷试验,发现小球落在不规则区域的频率稳定在常数0.65附近,由此可估计不规则区域的面积约为( )

A. 2.6m2 B. 5.6m2 C. 8.25m2 D. 10.4m2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个二次函数的图象,三位同学分别说出了它的一些特征:甲:对称轴是![]() ;乙:与
;乙:与![]() 轴两个交点的横坐标都是整数;丙:与
轴两个交点的横坐标都是整数;丙:与![]() 轴交点的纵坐标也是整数,且以这三个点为顶点的三角形面积为
轴交点的纵坐标也是整数,且以这三个点为顶点的三角形面积为![]() .请写出满足上述全部特征的一个二次函数的解析式.
.请写出满足上述全部特征的一个二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ;
(2)图2中,当∠D=50度,∠B=40度时,求∠P的度数.
(3)图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
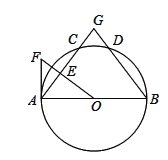
【题目】如图,AB是⊙O的直径,C、D为⊙O上两点,且![]() ,过点O作OE⊥AC于点E,⊙O的切线AF交OE的延长线于点F,弦AC、BD的延长线交于点G.
,过点O作OE⊥AC于点E,⊙O的切线AF交OE的延长线于点F,弦AC、BD的延长线交于点G.
(1)求证:∠F=∠B;
(2)若AB=10,BG=13,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
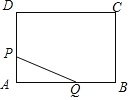
【题目】如图,矩形ABCD中,AB=8cm,BC=6cm,点P从点A出发,以lcm/s的速度沿A→D→C方向匀速运动,同时点Q从点A出发,以2cm/s的速度沿A→B→C方向匀速运动,当一个点到达点C时,另一个点也随之停止.设运动时间为t(s),△APQ的面积为S(cm2),下列能大致反映S与t之间函数关系的图象是( )
A. 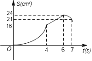 B.
B. 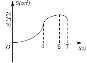 C.
C. 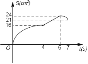 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
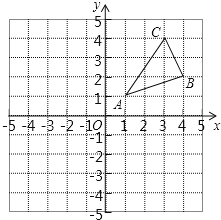
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC关于原点对称的△A1B1C1;
(2)四边形CBC1B1为 四边形;
(3)点P为平面内一点,若以点A、B、C、P为顶点的四边形为平行四边形,请直接写出所有满足条件的点P坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com