
| �� �� | 4�·� | 5�·� | 6�·� |
| ���ѽ�� | 40Ԫ | 45Ԫ | 57Ԫ |
���� ��1����0��x��20ʱ���շѱ��ǣ�2.5Ԫ/m3�Ʒѣ���x��20ʱ���շѱ��ǣ�����ˮ������20m3ʱ�����е�20m3��2.5Ԫ/m3�շѣ��������ְ�3.5Ԫ/m3�Ʒѣ��г�����ʽ���ɣ�
��2��������ɵã���Ϊ���·ݡ����·ݽɷѽ�����50Ԫ��������y=2.5x������ˮ�������·ݽɷѽ���50Ԫ��������y=3.5x-20������ˮ����
��� �⣺��1����0��x��20ʱ��y��x�ĺ�������ʽ�ǣ�y=2.5x��
��x��20ʱ��y��x�ĺ�������ʽ�ǣ�y=2.5��20+3.5��x-20��=3.5x-20��
�ʴ�Ϊ��2.5x��3.5x-20��
��2��С����4�·���ˮ��δ����20m3����2.5x=40��
��ã�x=16
С����5�·���ˮ��δ����20m3����2.5x=45��
x=18��
С����6�·���ˮ������20m3��3.5x-20=57��
��ã�x=22��
��С���ҵڶ����ȵ���ˮ��Ϊ��16+18+22=56��m3����
���� ���⿼�����д���ʽ������ͼ����Ϣ����ֶ��շѱ��ǽ���Ĺؼ����ѵ����ڸ��ݽ��ѽ���жϳ�������ˮ�����ڵĵ��Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 10 | B�� | 9 | C�� | 7 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 420Ԫ | B�� | 500Ԫ | C�� | 540Ԫ | D�� | 480Ԫ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ������a��b��c�������ϵ�λ����ͼ��ʾ����|a-c|-|a-b|-|b-c|=2a-2b��
������a��b��c�������ϵ�λ����ͼ��ʾ����|a-c|-|a-b|-|b-c|=2a-2b���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
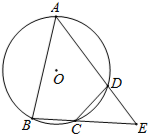 ��ͼ���ı���ABCD�ڽ��ڡ�O��BC���ӳ�����AD���ӳ����ཻ�ڵ�E����DC=DE����֤����A=��AEB��
��ͼ���ı���ABCD�ڽ��ڡ�O��BC���ӳ�����AD���ӳ����ཻ�ڵ�E����DC=DE����֤����A=��AEB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
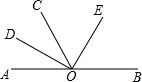 ��ͼ��AOB��һ��ֱ�ߣ���AOC=60�㣬OD��OE�ֱ��ǡ�AOC�͡�BOC��ƽ���ߣ���ͼ�л����Ľ��У�������
��ͼ��AOB��һ��ֱ�ߣ���AOC=60�㣬OD��OE�ֱ��ǡ�AOC�͡�BOC��ƽ���ߣ���ͼ�л����Ľ��У�������| A�� | 5�� | B�� | 6�� | C�� | 7�� | D�� | 8�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com