
【题目】综合与实践—探究正方形旋转中的数学问题
问题情境:已知正方形![]() 中,点
中,点![]() 在
在![]() 边上,且
边上,且![]() .将正方形
.将正方形![]() 绕点
绕点![]() 顺时针旋转得到正方形
顺时针旋转得到正方形![]() (点
(点![]() ,
,![]() ,
,![]() ,
,![]() 分别是点
分别是点![]() ,
,![]() ,
,![]() ,
,![]() 的对应点).同学们通过小组合作,提出下列数学问题,请你解答.
的对应点).同学们通过小组合作,提出下列数学问题,请你解答.
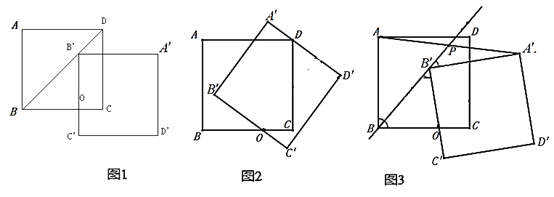
特例分析:(1)“乐思”小组提出问题:如图1,当点![]() 落在正方形
落在正方形![]() 的对角线
的对角线![]() 上时,设线段
上时,设线段![]() 与
与![]() 交于点
交于点![]() .求证:四边形
.求证:四边形![]() 是矩形;
是矩形;
(2)“善学”小组提出问题:如图2,当线段![]() 经过点
经过点![]() 时,猜想线段
时,猜想线段![]() 与
与![]() 满足的数量关系,并说明理由;
满足的数量关系,并说明理由;
深入探究:(3)请从下面![]() ,
,![]() 两题中任选一题作答.我选择题.
两题中任选一题作答.我选择题.
A.在图2中连接![]() 和
和![]() ,请直接写出
,请直接写出![]() 的值.
的值.
B.“好问”小组提出问题:如图3,在正方形![]() 绕点
绕点![]() 顺时针旋转的过程中,设直线
顺时针旋转的过程中,设直线![]() 交线段
交线段![]() 于点
于点![]() .连接
.连接![]() ,并过点
,并过点![]() 作
作![]() 于点
于点![]() .请在图3中补全图形,并直接写出
.请在图3中补全图形,并直接写出![]() 的值.
的值.
【答案】(1)见解析;(2)![]() ;(3)A.
;(3)A.![]() ,B.
,B.![]() .
.
【解析】
(1)根据旋转性质证得![]() ,从而证得绪论;
,从而证得绪论;
(2)连接![]() 、
、![]() ,过点
,过点![]() 作
作![]() ,根据旋转性质结合三角形三线合一的性质证得
,根据旋转性质结合三角形三线合一的性质证得![]() ,再证得四边形
,再证得四边形![]() 是矩形,从而求得结论;
是矩形,从而求得结论;
(3)A. 设![]() ,根据旋转性质结合两边对应成比例且夹角相等证得
,根据旋转性质结合两边对应成比例且夹角相等证得![]() ,利用相似三角形对应边成比例再结合勾股定理即可求得答案;
,利用相似三角形对应边成比例再结合勾股定理即可求得答案;
B. 作![]() 交直线
交直线![]() 于点
于点![]() ,根据旋转性质利用AAS证得
,根据旋转性质利用AAS证得![]() ,证得OP是线段
,证得OP是线段![]() 的中垂线,根据旋转性质结合两边对应成比例且夹角相等证得
的中垂线,根据旋转性质结合两边对应成比例且夹角相等证得![]() ,利用相似三角形对应高的比等于相似比再结合勾股定理即可求得答案;
,利用相似三角形对应高的比等于相似比再结合勾股定理即可求得答案;
(1)由题意得:![]() ,
,![]() ,
,
由旋转性质得:![]() ,
,
∵![]()
![]()
![]()
![]() 四边形
四边形![]() 是矩形
是矩形
(2)连接![]() 、
、![]() ,过点
,过点![]() 作
作![]() 于N,
于N,
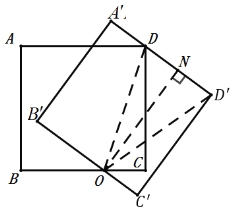
由旋转得:![]() ,
,
∵![]() ,
,
![]() ,
,
∵ON⊥D![]() ,∠
,∠![]() =∠
=∠![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]() ;
;
(3)A.如图,连接![]() ,
,![]() ,
,![]() ,
,
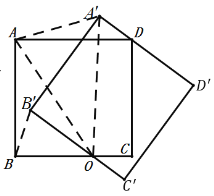
由旋转的性质得:∠BO![]() =∠
=∠![]() ,BO= O
,BO= O![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
![]()
![]()
B.如图,过点![]() 作AG∥
作AG∥![]() 交直线
交直线![]() 于点G,过点O作
于点G,过点O作![]() 交直线
交直线![]() 于点
于点![]() ,连接OP,
,连接OP,
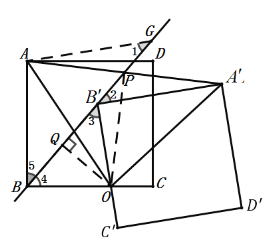
∵AG∥![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是正方形 ,
是正方形 ,
由旋转可知:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,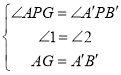
![]() ,
,
![]() ,
,
又∵![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
又∵![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 设
设![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,由勾股定理可得:
中,由勾股定理可得:
![]() ,
,
![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
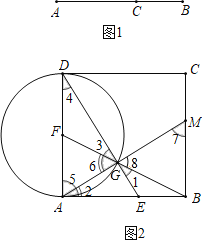
【题目】阅读下列材料,完成相应的学习任务:如图(1)在线段AB上找一点C,C把AB分为AC和BC两条线段,其中AC>BC.若AC,BC,AB满足关系AC2=BCAB.则点C叫做线段AB的黄金分割点,这时![]() =
=![]() ≈0.618,人们把
≈0.618,人们把![]() 叫做黄金分割数,我们可以根据图(2)所示操作方法我到线段AB的黄金分割点,操作步骤和部分证明过程如下:
叫做黄金分割数,我们可以根据图(2)所示操作方法我到线段AB的黄金分割点,操作步骤和部分证明过程如下:
第一步,以AB为边作正方形ABCD.
第二步,以AD为直径作⊙F.
第三步,连接BF与⊙F交于点G.
第四步,连接DG并延长与AB交于点E,则E就是线段AB的黄金分割点.
证明:连接AG并延长,与BC交于点M.
∵AD为⊙F的直径,
∴∠AGD=90°,
∵F为AD的中点,
∴DF=FG=AF,
∴∠3=∠4,∠5=∠6,
∵∠2+∠5=90°,∠5+∠4=90°,
∴∠2=∠4=∠3=∠1,
∵∠EBG=∠GBA,
∴△EBG∽△GBA,
∴![]() =
=![]() ,
,
∴BG2=BEAB…
任务:
(1)请根据上面操作步骤与部分证明过程,将剩余的证明过程补充完整;(提示:证明BM=BG=AE)
(2)优选法是一种具有广泛应用价值的数学方法,优选法中有一种0.618法应用了黄金分割数.为优选法的普及作出重要贡献的我国数学家是 (填出下列选项的字母代号)
A.华罗庚
B.陈景润
C.苏步青
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一菱形纸片ABCD,∠A=60°,将该菱形纸片折叠,使点A恰好与CD的中点E重合,折痕为FG,点F、G分别在边AB、AD上,联结EF,那么cos∠EFB的值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 为
为![]() 的直径,
的直径,![]() ,
,![]() 为
为![]() 上一动点(不与
上一动点(不与![]() 、
、![]() 重合).
重合).

(1)如图1,若![]() 平分
平分![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .①求证:
.①求证:![]() ;②若
;②若![]() ,求
,求![]() 的长;
的长;
(2)如图2,若![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得
得![]() ,连接
,连接![]() .求证:
.求证:![]() 为
为![]() 的切线.
的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示,请根据图表信息解答下列问题:
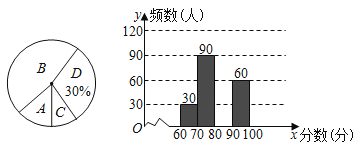
组别 | 分数段(分) | 频数 |
A组 | 60≤x<70 | 30 |
B组 | 70≤x<80 | 90 |
C组 | 80≤x<90 | m |
D组 | 90≤x<100 | 60 |
(1)本次调查的总人数为 人.
(2)补全频数分布直方图;
(3)若A组学生的平均分是65分,B组学生的平均分是75分,C组学生的平均分是85分,D出学生的平均分是95分,请你估计参加本次测试的同学们平均成绩是多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有黑、白两种颜色的球共50个,这些球除颜色外其余完全相同.王颖做摸球试验,搅匀后,她从盒子里随机摸出一个球记下颜色后,再把球放回盒子中,不断重复上述过程,如表是试验中的一组统计数据:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 65 | 124 | 178 | 302 | 480 | 600 | 1800 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.6 | 0.6 | 0.6 |
(1)请估计:当n很大时,摸到白球的频率将会接近 ;(精确到0.1)
(2)若从盒子里随机摸出一个球,则摸到白球的概率的估计值为 ;
(3)试估算盒子里黑、白两种颜色的球各有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“文明城市”活动周,活动周设置了“![]() :文明礼仪,
:文明礼仪,![]() :生态环境,
:生态环境,![]() :交通安全,
:交通安全,![]() :卫生保洁”四个主题活动,每个学生限选一个主题参与,为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下图所示的不完整的条形统计图和扇形统计图.
:卫生保洁”四个主题活动,每个学生限选一个主题参与,为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下图所示的不完整的条形统计图和扇形统计图.
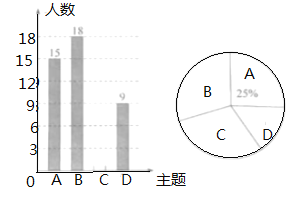
(1)本次随机调查的学生人数是_______人;
(2)补全条形统计图;
(3)在扇形统计图中,“![]() ”主题对应扇形的圆心角为________度.
”主题对应扇形的圆心角为________度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该商场两次共购进这种运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润不低于20%,那么每套售价至少是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com