
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,把线段
,把线段![]() 沿射线
沿射线![]() 方向平移(点
方向平移(点![]() 始终在射线
始终在射线![]() 上)至
上)至![]() 位置,直线
位置,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,又联结
,又联结![]() 与直线
与直线![]() 交于点
交于点![]() .
.
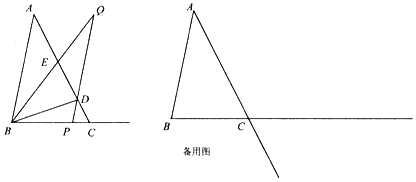
(1)当![]() 时,求证:
时,求证:![]() ;
;
(2)当点![]() 位于线段
位于线段![]() 上时(不含端点
上时(不含端点![]() 、
、![]() ),设
),设![]() ,
,![]() ,试求
,试求![]() 关于
关于![]() 的函数解析式,并写出定义域;
的函数解析式,并写出定义域;
(3)当以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似时,求
相似时,求![]() 的长.
的长.
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
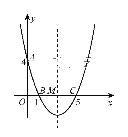
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
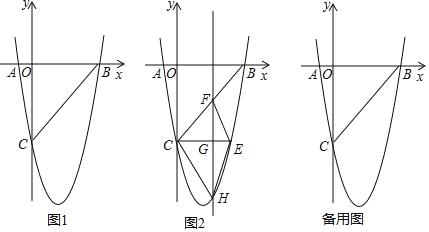
【题目】如图 1,在平面直角坐标系中,已知抛物线 y=ax2+bx﹣5 与 x 轴交于 A(﹣1,0),B(5, 0)两点,与 y 轴交于点 C.
(1)求抛物线的函数表达式;
(2)若点 D 是 y 轴上的一点,且以 B,C,D 为顶点的三角形与△ABC 相似,求点 D 的坐标;
(3)如图 2,CE∥x 轴与抛物线相交于点 E,点 H 是直线 CE 下方抛物线上的动点,过点 H且与 y 轴平行的直线与 BC,CE 分别相交于点 F,G,试探究当点 H 运动到何处时,四边形CHEF 的面积最大,求点 H 的坐标及最大面积;
(4)若点 K 为抛物线的顶点,点 M(4,m)是该抛物线上的一点,在 x 轴,y 轴上分别找点 P,Q,使四边形 PQKM 的周长最小,求出点 P,Q 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,2)请解答下列问题:
(1)画出△ABC关于y轴对称的△A1B1C1,并写出A1的坐标.
(2)画出△ABC绕点B逆时针旋转90°后得到的△A2B2C2,并写出A2的坐标.
(3)画出△A2B2C2关于原点O成中心对称的△A3B3C3,并写出A3的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《国家学生体质健康标准》规定:体质测试成绩达到90.0分及以上的为优秀;达到80.0分至89.9分的为良好;达到60.0分至79.9分的为及格;59.9分及以下为不及格,某校为了了解九年级学生体质健康状况,从该校九年级学生中随机抽取了10%的学生进行体质测试,测试结果如下面的统计表和扇形统计图所示。
各等级学生平均分统计表
等级 | 优秀 | 良好 | 及格 | 不及格 |
平均分 | 92.1 | 85.0 | 69.2 | 41.3 |
各等级学生人数分布扇形统计图

(1)扇形统计图中“不及格”所占的百分比是 ;
(2)计算所抽取的学生的测试成绩的平均分;
(3)若所抽取的学生中所有不及格等级学生的总分恰好等于某一个良好等级学生的分数,请估计该九年级学生中约有多少人达到优秀等级。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场销售某种冰箱,该种冰箱每台进价为2500元.已知原销售价为每台2900元时,平均每天能售出8台.若在原销售价的基础上每台降价50元,则平均每天可多售出4台.设每台冰箱的实际售价比原销售价降低了x元.
(1)填表(不需化简):
每天的销售量/台 | 每台销售利润/元 | |
降价前 | 8 | 400 |
降价后 |
(2)商场为使这种冰箱平均每天的销售利润达到5000元,则每台冰箱的实际售价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
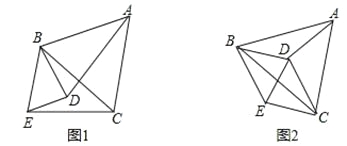
【题目】已知,如图1,△ABC中,BA=BC,D是平面内不与A、B、C重合的任意一点,∠ABC=∠DBE,BD=BE.
(1)求证:△ABD≌△CBE;
(2)如图2,当点D是△ABC的外接圆圆心时,请判断四边形BDCE的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D是BC边的中点,以D为顶点作一个120°的角,角的两边分别交直线AB,AC于M,N两点,以点D为中心旋转∠MDN(∠MDN的度数不变),若DM与AB垂直时(如图①所示),易证BM +CN =BD.
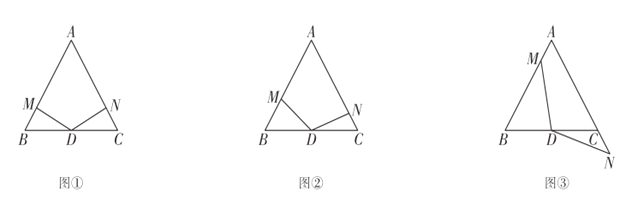
(1)如图②,若DM与AB不垂直时,点M在边AB上,点N在边AC上,上述结论是否成立?若成立,请给予证明;若不成立,请说明理由;
(2)如图③,若DM与AB不垂直时,点M在边AB.上,点N在边AC的延长线上,上述结论是否成立?若不成立,请写出BM,CN,BD之间的数量关系,不用证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某隧道横断面由抛物线与矩形的三边组成,尺寸如图所示.
(1)以隧道横断面抛物线的顶点为原点,以抛物线的对称轴为y轴,建立直角坐标系,求该抛物线对应的函数关系式;
(2)某卡车空车时能通过此隧道,现装载一集装箱箱宽3m,车与箱共高4.5m,此车能否通过隧道?并说明理由

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com