
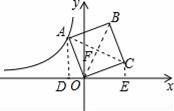
如图,在平面直角坐标系中,正方形ABCD的顶点O在坐标原点,点B的坐标为(1,4),点A在第二象限,反比例函数y=
 的图象经过点A,则k的值是( )
的图象经过点A,则k的值是( )


A.﹣2 B.﹣4 C.﹣
 D.
D.

C【考点】反比例函数图象上点的坐标特征.
【分析】作AD⊥x轴于D,CE⊥x轴于E,先通过证得△AOD≌△OCE得出AD=OE,OD=CE,设A(x,
 ),则C(
),则C(
 ,﹣x),根据正方形的性质求得对角线解得F的坐标,根据直线OB的解析式设出直线AC的解析式为:y=﹣
,﹣x),根据正方形的性质求得对角线解得F的坐标,根据直线OB的解析式设出直线AC的解析式为:y=﹣
 x+b,代入交点坐标求得解析式,然后把A,C的坐标代入即可求得k的值.
x+b,代入交点坐标求得解析式,然后把A,C的坐标代入即可求得k的值.
【解答】解:作AD⊥x轴于D,CE⊥x轴于E,
∵∠AOC=90°,
∴∠AOD+∠COE=90°,
∵∠AOD+∠OAD=90°,
∴∠OAD=∠COE,
在△AOD和△OCE中,

 ,
,
∴△AOD≌△OCE(AAS),
∴AD=OE,OD=CE,
设A(x,
 ),则C(
),则C(
 ,﹣x),
,﹣x),
∵点B的坐标为(1,4),
∴OB=
 =
=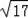
 ,
,
直线OB为:y=4x,
∵AC和OB互相垂直平分,
∴它们的交点F的坐标为(
 ,2),
,2),
设直线AC的解析式为:y=﹣
 x+b,
x+b,
代入(
 ,2)得,2=﹣
,2)得,2=﹣
 ×
×
 +b,解得b=
+b,解得b=
 ,
,
直线AC的解析式为:y=﹣
 x+
x+
 ,
,
把A(x,
 ),C(
),C(
 ,﹣x)代入得
,﹣x)代入得

 ,解得k=﹣
,解得k=﹣
 .
.
故选C.

【点评】本题考查了反比例函数图象上点的坐标特征,待定系数法求解析式,正方形的性质,三角形求得的判定和性质,熟练掌握正方形的性质是解题的关键.


科目:初中数学 来源: 题型:
阅读下列材料:
(1)关于x的方程x2﹣3x+1=0(x≠0)方程两边同时乘以
 得:
得:
 即
即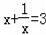
 ,
,



(2)a3+b3=(a+b)(a2﹣ab+b2);a3﹣b3=(a﹣b)(a2+ab+b2).
根据以上材料,解答下列问题:
(1)x2﹣4x+1=0(x≠0),则
 = 4 ,
= 4 ,
 = 14 ,
= 14 ,
 = 194 ;
= 194 ;
(2)2x2﹣7x+2=0(x≠0),求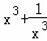
 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,AB=AC=13厘米,BC=10厘米,AD⊥BC于点D,动点P从点A出发以每秒1厘米的速度在线段AD上向终点D运动.设动点运动时间为t秒.

(1)求AD的长;
(2)当△PDC的面积为15平方厘米时, 求t的值;
求t的值;
(3)动点M从点C出发以每秒2厘米的速度在射线CB上运动.点M与点P同时出发,且当点P运动到终点D时,点M也停止运动.是否存在t,使得S△PMD= S△ABC?若存在,请求出t的值;若不存在,请说明理由.
S△ABC?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
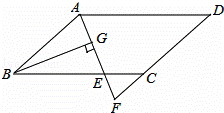
如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于
点E,交DC的延长线于点F,BG⊥AE于G,BG=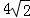 ,则梯形AECD的
,则梯形AECD的
周长( )
A.22 B.23 C.24 D.25
查看答案和解析>>
科目:初中数学 来源: 题型:
大双,小双的妈妈申购到一张北京奥运会的门票,兄弟俩决定分别用标有数字且除数字以外没有其它任何区别的小球,各自设计一种游戏确定谁去.
大双:A袋中放着分别标有数字1,2,3的三个小球,B袋中放着分别标有数字4,5的两个小球,且都已各自搅匀,小双蒙上眼睛从两个口袋中各取出1个小球,若两个小球上的数字之积为偶数,则大双得到门票;若积为奇数,则小双得到门票.
小双:口袋中放着分别标有数字1,2,3的三个小球,且已搅匀,大双,小双各蒙上眼睛有放回地摸1次,大双摸到偶数就记2分,摸到奇数记0分;小双摸到奇数就记1分,摸到偶数记0分,积分多的就得到门票.(若积分相同,则重复第二次.)
(1)大双设计的游戏方案对双方是否公平?请你运用列表或树状图说明理由;
(2)小双设计的游戏方案对双方是否公平?不必说理.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com