分解因式:a3b-2a2b2+ab3= ．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

分解因式：a3b-2a2b2+ab3= ．

练习册系列答案

典元教辅小学毕业升学必备小升初押题卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源：2015-2016学年湖北省等七年级上第一次联考数学试卷（解析版） 题型：选择题

比较下列各组数的大小（填“>”“<”或“=”）：

（1）-_______0；（2）-3．14______-3．15；（3）-（-5）_____|-5|．

查看答案和解析>>

科目：初中数学 来源：2014-2015学年浙江省杭州市5月中考模拟数学试卷（解析版） 题型：解答题

（1）计算：

（2）解分式方程：．

查看答案和解析>>

科目：初中数学 来源：2014-2015学年山东省威海市乳山市中考一模数学试卷（解析版） 题型：计算题

如图1，将一个直角三角板的直角顶点P放在正方形ABCD的对角线BD上滑动，并使其一条直角边始终经过点A，另一条直角边与BC相交于点E．

（1）求证：PA=PE；

（2）若将（1）中的正方形变为矩形，其余条件不变（如图2），且AD=10，DC=8，求AP：PE；

（3）在（2）的条件下，当P滑动到BD的延长线上时（如图3），请你直接写出AP：PE的比值．

【答案】（1）证明见解析；（2）AP：PE=5：4；（3）AP：PE=5：4；

【解析】

试题分析：（1）过P作PM⊥AB于M，PN⊥BC于N，四边形BMPN是正方形，得出PM=PN，∠MPN=90°，求出∠APM=∠NPE，∠AMP=∠PNE，证△APM≌△EPN，推出AP=PE即可；

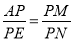（2）证△BPM∽△BDA，△BNP∽△BCD，得出，，推出，求出，证△APM∽△EPN，推出即可；

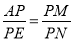（3）过P作PM⊥AB于M，PN⊥BC于N，证△BPM∽△BDA，△BNP∽△BCD，得出，，推出，求出，证△APM∽△EPN，推出即可．

试题解析：（1）证明：过P作PM⊥AB于M，PN⊥BC于N，

∵四边形ABCD是正方形，

∴∠ABD=45°，

∴∠MPB=45°=∠ABD，

∴PM=BM，

同理BP=BN，

∵四边形ABCD是正方形，

∴∠ABC=90°=∠BMP=∠BNP，

∴四边形BMPN是正方形，

∴PM=PN，∠MPN=90°，

∵∠APE=90°，

∴都减去∠MPE得：∠APM=∠NPE，

∵PM⊥AB，PN⊥BC，

∴∠AMP=∠PNE，

在△APM和△EPN中

∴△APM≌△EPN（ASA），

∴AP=PE；

（2）【解析】
∵四边形ABCD是矩形，

∴∠BAD=∠C=90°，

∵∠PMB=PNB=90°，

∴PM∥AD，PN∥CD，

∴△BPM∽△BDA，△BNP∽△BCD，

∴，，，

∴，

∵∠AMP=∠ENP=90°，∠MPA=∠EPN，

∴△APM∽△EPN，

∴=，

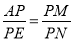AP：PE=5：4；

（3）【解析】
AP：PE=5：4．

考点：相似形综合题．

【题型】解答题
【适用】一般
【标题】2015届山东省威海市乳山市中考一模数学试卷（带解析）
【关键字标签】
【结束】

如图，直线y=-x+2与x轴交于点B，与y轴交于点C，已知二次函数的图象经过点B，C和点A（-1，0）．

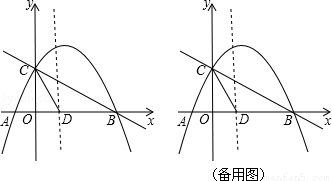
（1）求B，C两点坐标；

（2）求该二次函数的关系式；

（3）若抛物线的对称轴与x轴的交点为点D，点E是线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标；

（4）在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明问题．

查看答案和解析>>

科目：初中数学 来源：2014-2015学年山东省威海市乳山市中考一模数学试卷（解析版） 题型：填空题

在直角坐标系xOy中，对于点P（x，y），我们把点P′（y+1，-x+1）叫做点P的影子点．已知点A1的影子点为A2，点A2的影子点为A3，点A3的影子点为A4，…，这样依次得到点A1，A2，A3，…，An，…若点A1的坐标为（a，b），对于任意的正整数n，点An均在y轴的右侧，则a，b应满足的条件是．

查看答案和解析>>

科目：初中数学 来源：2014-2015学年山东省威海市乳山市中考一模数学试卷（解析版） 题型：选择题

某工厂现在平均每天比原计划多生产30台机器，现在生产500台机器所需时间与圆计划生产350台机器所需时间相同．设原计划平均每天生产x台机器，下面所列方程正确的是（）

A． B．