
如图,在矩形ABCD中,AB=3cm,BC=4cm.设P、Q分别为BD、BC上的动点,在点P自点D沿DB方向作匀速移动的同时,点Q自点B沿BC方向向点C作匀速移动,移动的速度均为1cm/s,设P、Q的移动时间为t(0<t≤4)
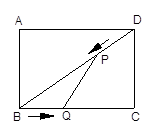
1.求△PBQ的面积S(cm2)与时间t(s)之间的函数关系式;
2.是否存在时刻t,使△PBQ的面积与四边形CDPQ的面积相等?若有,请求出时间t的
值;若没有,请说明理由;
3.当t为何值时,△PBQ为等腰三角形?并判断△PBQ能否
成为等边三角形?
1.
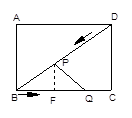
∵矩形ABCD中,AB=3cm,BC=4cm
∴CD= AB=3cm
∴在Rt△BCD中 BD=5cm
由题意得:PD=t,BQ=t,BP=5-t
过P作PE⊥BC于E,则PE∥CD
∴△BPE∽△BDC ∴![]() 即
即![]()
∴![]() 2分
2分
∴![]()
![]()
![]() 3分
3分
2.不存在t满足条件
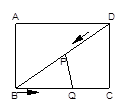
∵![]() ∴
∴![]() 时,有
时,有 ![]()
∵![]()
∴令![]() ,则有
,则有![]() 即
即![]() 5分
5分
∵![]() ∴方程无实数根
∴方程无实数根
∴不存在满足条件的t 6分
3.若BP=PQ 则过P作PF⊥BC于F
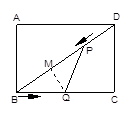
∴PF∥CD BF=QF=![]()
∴△BPF∽△BDC ∴![]()
即![]() ∴
∴![]()
若BP=QB,则![]() ∴
∴![]()
若QB=PQ,则过Q作QM⊥BD于M
∴∠BMQ=∠C=90° BM=PM=![]() BP
BP
∵∠CBD=∠CBD ∴△BMQ∽△BDC
∴![]() 即
即![]() ∴
∴![]()
∴![]() ,
,![]() ,
,![]() 时,△PBQ为等腰三角形 9分
时,△PBQ为等腰三角形 9分
△PBQ不能为等边三角形 10分
解析:略


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
 如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点A出发以1cm/s的速度向点B运动,点Q从点B出发以2cm/s的速度向点C运动,设经过的时间为xs,△PBQ的面积为ycm2,则下列图象能反映y与x之间的函数关系的是( )
如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点A出发以1cm/s的速度向点B运动,点Q从点B出发以2cm/s的速度向点C运动,设经过的时间为xs,△PBQ的面积为ycm2,则下列图象能反映y与x之间的函数关系的是( )A、 | B、 | C、 | D、 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 .
.| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 动过程中,Q点停留了1s,图②是P、Q两点在折线AB-BC-CD上相距的路程S(cm)与时间t(s)之间的函数关系图象.
动过程中,Q点停留了1s,图②是P、Q两点在折线AB-BC-CD上相距的路程S(cm)与时间t(s)之间的函数关系图象.查看答案和解析>>
科目:初中数学 来源: 题型:
 DE,EF与AB交于点F,设CE=x,BF=y.
DE,EF与AB交于点F,设CE=x,BF=y.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com