
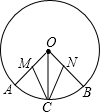
 已知如图所示,OA、OB、OC是⊙O的三条半径,弧AC和弧BC相等,M、N分别是OA、OB的中点.求证:MC=NC.
已知如图所示,OA、OB、OC是⊙O的三条半径,弧AC和弧BC相等,M、N分别是OA、OB的中点.求证:MC=NC. 分析 根据弧与圆心角的关系,可得∠AOC=∠BOC,又由M、N分别是半径OA、OB的中点,可得OM=ON,利用SAS判定△MOC≌△NOC,继而证得结论.
解答 证明:∵弧AC和弧BC相等,
∴∠AOC=∠BOC,
又∵OA=OB M、N分别是OA、OB的中点
∴OM=ON,
在△MOC和△NOC中,$\left\{\begin{array}{l}{OM=ON}&{\;}\\{∠AOC=∠BOC}&{\;}\\{OC=OC}&{\;}\end{array}\right.$,
∴△MOC≌△NOC(SAS),
∴MC=NC.
点评 此题考查了弧与圆心角的关系以及全等三角形的判定与性质;证明三角形全等是解决问题的关键.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:解答题
| 进价(元/只) | 售价(元/只) | |
| 甲型 | 25 | 30 |
| 乙型 | 45 | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 从一定高度落下的图钉落地后顶尖朝上 | |
| B. | 打开数学课本时刚好翻到第60页 | |
| C. | 早晨太阳一定从东方升起 | |
| D. | 今年14岁的小明一定是初中学生 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com