
【题目】已知在扇形![]() 中,圆心角
中,圆心角![]() ,半径
,半径![]() .
.
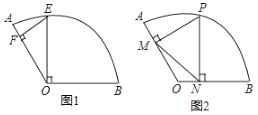
(1)如图1,过点![]() 作
作![]() ,交弧
,交弧![]() 于点
于点![]() ,再过点
,再过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() 的长为_________,
的长为_________,![]() 的度数为_________;
的度数为_________;
(2)如图2,设点![]() 为弧
为弧![]() 上的动点,过点
上的动点,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,点
,点![]() 分别在半径
分别在半径![]() ,
,![]() 上,连接
上,连接![]() ,则
,则
①求点![]() 运动的路径长是多少?
运动的路径长是多少?
②![]() 的长度是否是定值?如果是,请求出这个定值;若不是,请说明理由;
的长度是否是定值?如果是,请求出这个定值;若不是,请说明理由;
(3)在(2)中的条件下,若点![]() 是
是![]() 的外心,直接写出点
的外心,直接写出点![]() 运动的路经长.
运动的路经长.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ;②是定值,为
;②是定值,为![]() ;(3)
;(3)![]()
【解析】
(1)先求出∠AOE,再解直角三角形,即可得出结论;
(2)①当点M与点O重合时,∠PMB=30°,当点N与点O重合时,∠PNA=30°,进而求出点P运动路径所对的圆心角是120°-30°-30°=60°,最后用弧长公式即可得出结论;
②先判断出点P,M,O,N四点均在同一个圆,即⊙H上,进而求出MK=![]() ,即可得出结论;
,即可得出结论;
(3)先判断出三角形PMN的外接圆的圆心的运动轨迹,最后根据弧长公式即可得出结论.
解:(1)∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
在![]() 中,
中,![]() .
.
∴![]() ,
,![]() ,
,
故答案为:![]() ,
,![]()
(2)①点![]() 在弧
在弧![]() 上运动,其路径也是一段弧,由题意可知,
上运动,其路径也是一段弧,由题意可知,
当点![]() 与点
与点![]() 重合时,
重合时,![]() ,
,
当点![]() 与点
与点![]() 重合时,
重合时,![]() ,
,
∴点![]() 运动路径所对的圆心角是
运动路径所对的圆心角是![]() ,
,
∴点![]() 运动的路径长
运动的路径长![]() ;
;
②是定值;
连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
∵在![]() 和
和![]() 中,点
中,点![]() 是斜边
是斜边![]() 的中点,
的中点,
∴![]() ,
,
∴根据圆的定义可知,点![]() 四点均在同一个圆,即
四点均在同一个圆,即![]() 上,
上,
又∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,
,
由垂径定理得,![]() ,
,
∴在![]() 中,
中,![]() ,
,![]() ,则
,则![]() ,
,
∴![]() ,是定值.
,是定值.
(3)由(2)知,点![]() 四点共圆,
四点共圆,
∴![]() 是
是![]() 的外接圆的圆心,即:点
的外接圆的圆心,即:点![]() 和点
和点![]() 重合,
重合,
∴![]() ,
,
∴点![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径,
为半径,
∴点![]() 运动路径所对的圆心角是
运动路径所对的圆心角是![]() ,
,
∴点![]() 运动路径所对的圆心角是
运动路径所对的圆心角是![]() ,
,
∴点![]() 运动的路经长为
运动的路经长为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD为矩形,曲线L经过点D.点Q是四边形ABCD内一定点,点P是线段AB上一动点,作PM⊥AB交曲线L于点M,连接QM.
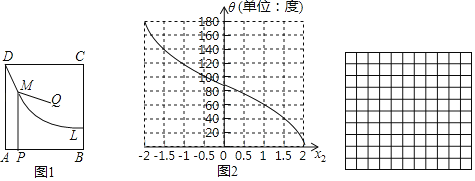
小东同学发现:在点P由A运动到B的过程中,对于x1=AP的每一个确定的值,θ=∠QMP都有唯一确定的值与其对应,x1与θ的对应关系如表所示:
x1=AP | 0 | 1 | 2 | 3 | 4 | 5 |
θ=∠QMP | α | 85° | 130° | 180° | 145° | 130° |
小芸同学在读书时,发现了另外一个函数:对于自变量x2在﹣2≤x2≤2范围内的每一个值,都有唯一确定的角度θ与之对应,x2与θ的对应关系如图2所示:
根据以上材料,回答问题:
(1)表格中α的值为 .
(2)如果令表格中x1所对应的θ的值与图2中x2所对应的θ的值相等,可以在两个变量x1与x2之间建立函数关系.
①在这个函数关系中,自变量是 ,因变量是 ;(分别填入x1和x2)
②请在网格中建立平面直角坐标系,并画出这个函数的图象;
③根据画出的函数图象,当AP=3.5时,x2的值约为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点![]() 为
为![]() 边上的一个动点.
边上的一个动点.
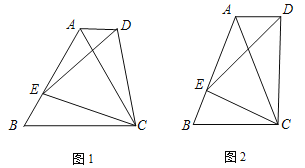
(1)如图1,若![]() 是等边三角形,以
是等边三角形,以![]() 为边在
为边在![]() 的同侧作等边
的同侧作等边![]() ,连接
,连接![]() .试比较
.试比较![]() 与
与![]() 的大小,并说明理由;
的大小,并说明理由;
(2)如图2,若![]() 中,
中,![]() ,以
,以![]() 为底边在
为底边在![]() 的同侧作等腰
的同侧作等腰![]() ,且
,且![]() ∽
∽![]() ,连接
,连接![]() .试判断
.试判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
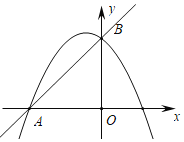
【题目】在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 、
、![]() .
.
(1)求![]() 、
、![]() 满足的关系式及
满足的关系式及![]() 的值.
的值.
(2)当![]() 时,若
时,若![]() 的函数值随
的函数值随![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
(3)如图,当![]() 时,在抛物线上是否存在点
时,在抛物线上是否存在点![]() ,使
,使![]() 的面积为1?若存在,请求出符合条件的所有点
的面积为1?若存在,请求出符合条件的所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图图形都是由同样大小的正方形“□”按照一定规律排列的,其中图①中共有2个正方形,图②中共有4个正方形,图③中共有7个正方形,图④中共有12个正方形,图⑤中共有21个正方形,……,照此规律排列下去,则图⑩中正方形的个数为_____.
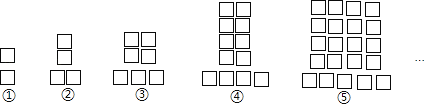
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中直线y=x﹣2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).

(1)求反比例函数的关系式;
(2)将直线y=x﹣2向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 和点
和点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 是线段
是线段![]() 上的一个动点.设点
上的一个动点.设点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交抛物线于点
交抛物线于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
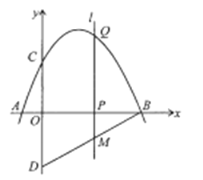
(1)求抛物线的解析式;
(2)连接![]() ,
,![]() ,当点
,当点![]() 运动到何处时,
运动到何处时,![]() 面积最大?最大面积是多少?并求出此时点
面积最大?最大面积是多少?并求出此时点![]() 的坐标;
的坐标;
(3)在第![]() 问的前提下,在
问的前提下,在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 值最小,求出
值最小,求出![]() 的最小值并直接写出此时点
的最小值并直接写出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,点
中,点![]() . 沿直线
. 沿直线![]() 折叠矩形
折叠矩形![]() ,使点
,使点![]() 落在
落在![]() 边上,与点
边上,与点![]() 重合.分别以
重合.分别以![]() ,
,![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 轴建立平面直角坐标系,抛物线
轴建立平面直角坐标系,抛物线![]() 经过
经过![]() 两点.
两点.
(1)求![]() 及点
及点![]() 的坐标;
的坐标;
(2)一动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒
以每秒![]() 个单位长的速度向点
个单位长的速度向点![]() 运动, 同时动点
运动, 同时动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒
以每秒![]() 个单位长的速度向点
个单位长的速度向点![]() 运动, 当点
运动, 当点![]() 运动到点
运动到点![]() 时,两点同时停止运动.设运动时间为
时,两点同时停止运动.设运动时间为![]() 秒,当
秒,当![]() 为何值时,以
为何值时,以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
(3)点![]() 在抛物线对称轴上,点
在抛物线对称轴上,点![]() 在抛物线上,是否存在这样的点
在抛物线上,是否存在这样的点![]() 与点 N,使以
与点 N,使以![]() ,
,![]() ,
,![]() ,
, ![]() 为顶点的四边形是平行四边形?若存在,请直接写出点
为顶点的四边形是平行四边形?若存在,请直接写出点![]() 与点
与点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
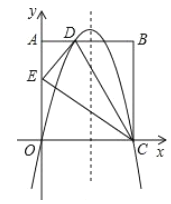
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com