
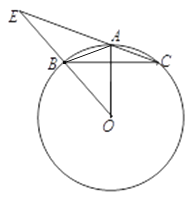
【题目】如图,△ABC内接于⊙O,AB=AC,连接并延长OB交CA延长线于点E.
(1)求证: OA平分∠BAC;
(2)若tan∠ABC=![]() ,AC=
,AC=![]() . 求⊙O的半径和线段BE的长.
. 求⊙O的半径和线段BE的长.
【答案】(1)见解析;(2)![]()
【解析】分析:(1)连接OC.由AB=AC,得到弧AB=弧AC ,从而得到∠AOB=∠AOC .由等腰三角形的性质得到OA⊥BC,即可得出结论.
(2)延长AO交圆于P ,连接PC.由tan∠P=tan∠ABC=![]() ,得到PC,AP的长,即可得到半径.证明△EBA∽△EAO,得到
,得到PC,AP的长,即可得到半径.证明△EBA∽△EAO,得到 ![]() .设BE=
.设BE=![]() x,则AE=5x,OE=OB+BE=5+
x,则AE=5x,OE=OB+BE=5+![]() x,得到
x,得到![]() ,解方程即可得到结论.
,解方程即可得到结论.
详解:(1)连接OC.
∵AB=AC,∴弧AB=弧AC ,∴∠AOB=∠AOC .
∵OB=OC, ∴OA⊥BC.
∵AB=AC,∴OA平分∠BAC.
(2)延长AO交圆于P ,连接PC.tan∠P=tan∠ABC=![]() ,
,
∴PC=3AC=![]() ,AP=10,∴r=5.
,AP=10,∴r=5.
∵AB=AC,∴∠ABC=∠ACB.
∵∠EAB=∠ABC+∠ACB=2∠ACB=∠AOB,∠E=∠E,
∴△EBA∽△EAO,∴ ![]() .
.
设BE=![]() x,则AE=5x,OE=OB+BE=5+
x,则AE=5x,OE=OB+BE=5+![]() x,
x,
∴![]() ,解得:x=
,解得:x=![]() ,∴BE=
,∴BE=![]() x=
x=![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=∠C=90°,∠B=α,在AB,BC上分别找一点E,F,使△DEF的周长最小,此时,∠EDF=______。(用含α的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的图形是由边长为l的正方形按照某种规律排列而组成的.
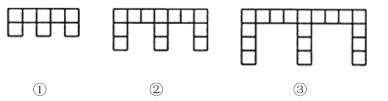
(1)观察图形,填写下表:

(2)推测第n个图形中,正方形的个数为 ,周长为 (都用含n的代数式表示).
(3)这些图形中,任意一个图形的周长y与它所含正方形个数x之间的关系可表示为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(﹣2,0),点B(6,0),点C在第一象限内,且△OBC为等边三角形,直线BC交y轴于点D,过点A作直线AE⊥BD于点E,交OC于点E
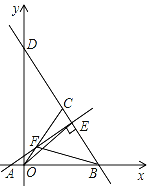
(1)求直线BD的解析式;(2)求线段OF的长;(3)求证:BF=OE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠D=90°,AB=13,BC=12,CD=4,AD=3.

求:(1)AC的长度;
(2)判断△ACB是什么三角形?并说明理由?
(3)四边形ABCD的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数形结合是数学解题中的一种重要思想,利用数轴可以将数与形完美结合.一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|,如:数轴上表示4和1的两点之间的距离是|4﹣1|=3;表示﹣3和2两点之间的距离是|﹣3﹣2|=5.
![]()
根据以上材料,结合数轴与绝对值的知识回答下列问题:
(1)将数﹣5,﹣![]() ,0,2.5在数轴上表示出来.
,0,2.5在数轴上表示出来.
(2)若数轴上表示数a的点位于﹣3与2之间,那么|a+3|+|a﹣2|的值是多少?
(3)若A是数轴上的一个点,它表示数a,则|a+5|+|a﹣3|的最小值是多少?当a取多少时|a+5|+|a﹣1|+|a﹣3|有最小值?最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体校要从四名射击选手中选拔一名参加省体育运动会,选拔赛中每名选手连续射靶10次,他们各自的平均成绩![]() 及其方差S2如表所示:
及其方差S2如表所示:
甲 | 乙 | 丙 | 丁 | |
(环) | 8.4 | 8.6 | 8.6 | 7.6 |
S2 | 0.74 | 0.56 | 0.94 | 1.92 |
如果要选出一名成绩高且发挥稳定的选手参赛,则应选择的选手是( )
A.甲 B.乙 C.丙 D.丁
查看答案和解析>>
科目:初中数学 来源: 题型:
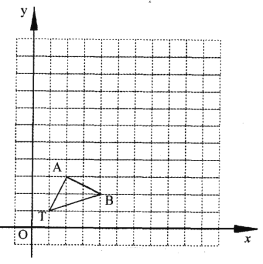
【题目】如图,在正方形网格中,△TAB 的顶点坐标分别为 T(1,1)、A(2,3)、B(4,2).
(1)以点 T(1,1)为位似中心,在位似中心的 同侧将△TAB 放大为原来的 3 倍,放大 后点 A、B 的对应点分别为 A'、B',画出△TA'B':
(2)写出点 A'、B'的坐标:A'( )、B'( );
(3)在(1)中,若 C(a,b)为线段 AB 上任一 点,则变化后点 C 的对应点 C'的坐标为 ( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是明明设计的智力拼图玩具的一部分,现在明明遇到了两个问题,请你帮助解决:
问题1:∠D=32°,∠ACD=60°,为保证AB∥DE,则∠A等于多少度?
问题2:∠G,∠GFH,∠H之间有什么样的关系时,GP∥HQ?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com