
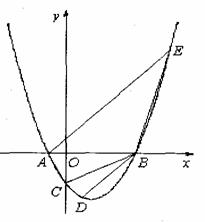
设抛物线![]() 与x轴交于两个不同的点A(-1,0)、B(m,0),与y轴交于点C.且∠ACB=90°.
与x轴交于两个不同的点A(-1,0)、B(m,0),与y轴交于点C.且∠ACB=90°.
(1)求m的值;
(2)求抛物线的解析式,并验证点D(1,-3 )是否在抛物线上;
(3)已知过点A的直线![]() 交抛物线于另一点E. 问:在x轴上是否存在点P,使以点P、B、D为顶点的三角形与△AEB相似?若存在,请求出所有符合要求的点P的坐标. 若不存在,请说明理由.
交抛物线于另一点E. 问:在x轴上是否存在点P,使以点P、B、D为顶点的三角形与△AEB相似?若存在,请求出所有符合要求的点P的坐标. 若不存在,请说明理由.
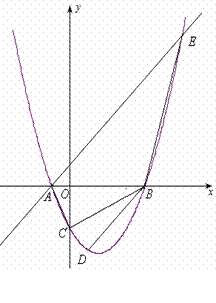 |
解:(1)令x=0,得y=-2 ∴C(0,-2)
∵∠ACB=90°,CO⊥AB ,∴△AOC ∽△COB ,∴OA?OB=OC2
∴OB=![]() ∴m=4
∴m=4
(2)将A(-1,0),B(4,0)代入![]() ,解得
,解得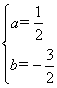
∴抛物线的解析式为![]()
当x=1时,![]() =-3,∴点D(1,-3)在抛物线上。
=-3,∴点D(1,-3)在抛物线上。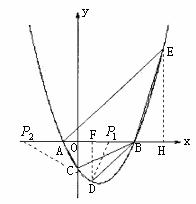 (3)由
(3)由![]() 得
得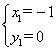
![]() ,∴E(6,7)
,∴E(6,7)
过E作EH⊥x轴于H,则H(6,0),
∴ AH=EH=7 ∴∠EAH=45°
作DF⊥x轴于F,则F(1,0)
∴BF=DF=3 ∴∠DBF=45°
∴∠EAH=∠DBF=45°
∴∠DBH=135°,90°<∠EBA<135°
则点P只能在点B的左侧,有以下两种情况:
①若△DBP1∽△EAB,则![]() ,∴
,∴![]()
∴![]() ,∴
,∴![]()
②若△![]() ∽△BAE,则
∽△BAE,则![]() ,∴
,∴![]()
∴![]() ∴
∴![]()
综合①、②,得点P的坐标为:![]()


科目:初中数学 来源: 题型:
设抛物线![]() 与x轴交于两个不同的点A(一1,0)、B(m,0),与y轴交于点C.且∠ACB=90°.
与x轴交于两个不同的点A(一1,0)、B(m,0),与y轴交于点C.且∠ACB=90°.
(1)求m的值和抛物线的解析式;
(2)已知点D(1,n )在抛物线上,过点A的直线![]() 交抛物线于另一点E.若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标.
交抛物线于另一点E.若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标.
(3)在(2)的条件下,△BDP的外接圆半径等于________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
(本题满分12分)
设抛物线与X轴交于两不同的点
(点A在点B的左边),与y轴的交点为点C(0,-2),且∠ACB=900.
1.(1)求m的值和该抛物线的解析式;
2.(2)若点D为该抛物线上的一点,且横坐标为1,点E为过A点的直线y=x+1与该抛物线的另一交点.在X轴上是否存在点P,使得以P、B、D为顶点的三角形与△AEB相似,若存在,求出点P的坐标,若不存在,请说明理由.
3.(3)连结AC、BC,矩形FGHQ的一边FG在线段AB上,顶点H、Q分别在线段AC、BC上,若设F点坐标为(t,0),矩形FGHQ的面积为S,当S取最大值时,连接FH并延长至点M,使HM=k·FH,若点M不在该抛物线上,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源:2010年四川省成都武侯区中考模拟试题数学卷 题型:填空题
(本题满分12分)
设抛物线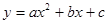 与X轴交于两不同的点
与X轴交于两不同的点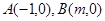 (点A在点B的左边),与y轴的交点为点C(0,-2),且∠ACB=900.
(点A在点B的左边),与y轴的交点为点C(0,-2),且∠ACB=900.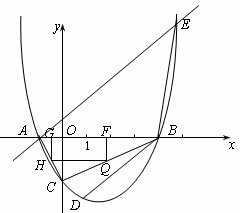
【小题1】(1)求m的值和该抛物线的解析式;
【小题2】(2)若点D为该抛物线上的一点,且横坐标为1,点E为过A点的直线y=x+1与该抛物线的另一交点.在X轴上是否存在点P,使得以P、B、D为顶点的三角形与△AEB相似,若存在,求出点P的坐标,若不存在,请说明理由.
【小题3】(3)连结AC、BC,矩形FGHQ的一边FG在线段AB上,顶点H、Q分别在线段AC、BC上,若设F点坐标为(t,0),矩形FGHQ的面积为S,当S取最大值时,连接FH并延长至点M,使HM=k·FH,若点M不在该抛物线上,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源:2010年四川省考模拟试题数学卷 题型:填空题
(本题满分12分)
设抛物线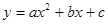 与X轴交于两不同的点
与X轴交于两不同的点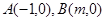 (点A在点B的左边),与y轴的交点为点C(0,-2),且∠ACB=900.
(点A在点B的左边),与y轴的交点为点C(0,-2),且∠ACB=900.
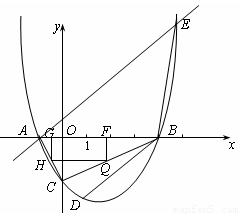
1.(1)求m的值和该抛物线的解析式;
2.(2)若点D为该抛物线上的一点,且横坐标为1,点E为过A点的直线y=x+1与该抛物线的另一交点.在X轴上是否存在点P,使得以P、B、D为顶点的三角形与△AEB相似,若存在,求出点P的坐标,若不存在,请说明理由.
3.(3)连结AC、BC,矩形FGHQ的一边FG在线段AB上,顶点H、Q分别在线段AC、BC上,若设F点坐标为(t,0),矩形FGHQ的面积为S,当S取最大值时,连接FH并延长至点M,使HM=k·FH,若点M不在该抛物线上,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com