
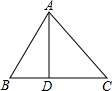
 如图,△ABC中,AB=12,BC=15,AD⊥BC于点D,∠BAD=30°,求tanC的值.
如图,△ABC中,AB=12,BC=15,AD⊥BC于点D,∠BAD=30°,求tanC的值. 分析 根据在△ABC中,AB=12,BC=15,AD⊥BC于点D,∠BAD=30°,可以求得BD、AD、CD的长,从而可以求得tanC的值.
解答 解:∵△ABC中,AB=12,BC=15,AD⊥BC于点D,∠BAD=30°,
∴∠ADB=∠ADC=90°,
∴AB=2BD,
∴BD=6,
∴CD=BC-BD=15-6=9,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}=\sqrt{1{2}^{2}-{6}^{2}}=6\sqrt{3}$,
∴tanC=$\frac{AD}{CD}=\frac{6\sqrt{3}}{9}=\frac{2\sqrt{3}}{3}$.
即tanC的值是$\frac{2\sqrt{3}}{3}$.
点评 本题考查解直角三角形,解题的关键是计算出题目中各边的长,找出所求问题需要的条件.


科目:初中数学 来源: 题型:解答题
 为了解我省2015届九年级学生学业水平考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:0-29分;B:30-39分;C:40-44分;D:45-49分;E:50分)统计如下:
为了解我省2015届九年级学生学业水平考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:0-29分;B:30-39分;C:40-44分;D:45-49分;E:50分)统计如下:| 分数段 | 人数(人) | 频率 |
| A | 12 | 0.05 |
| B | 36 | b |
| C | 84 | 0.35 |
| D | a | 0.25 |
| E | 48 | 0.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com