
【题目】如图,已知正方形ABCD,点E为AB上的一点,EF⊥AB,交BD于点F.
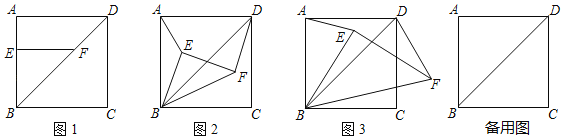
(1)如图1,直按写出![]() 的值 ;
的值 ;
(2)将△EBF绕点B顺时针旋转到如图2所示的位置,连接AE、DF,猜想DF与AE的数量关系,并证明你的结论;
(3)如图3,当BE=BA时,其他条件不变,△EBF绕点B顺时针旋转,设旋转角为α(0°<α<360°),当α为何值时,EA=ED?在图3或备用图中画出图形,并直接写出此时α= .
【答案】(1)![]() ;(2)DF=
;(2)DF=![]() AE,理由见解析;(3)作图见解析,30°或150°
AE,理由见解析;(3)作图见解析,30°或150°
【解析】
(1)直接利用等腰直角三角形的性质计算即可得出结论;
(2)先判断出![]() ,进而得出△ABE∽△DBF,即可得出结论;
,进而得出△ABE∽△DBF,即可得出结论;
(3)先判断出点E在AD的中垂线上,再判断出△BCE是等边三角形,求出∠CBE=60°,再分两种情况计算即可得出结论.
(1)∵BD是正方形ABCD的对角线,
∴∠ABD=45![]() ,BD=
,BD=![]() AB,
AB,
∵EF⊥AB,
∴∠BEF=90![]() ,
,
∴∠BFE=∠ABD=45![]() ,
,
∴BE=EF,
∴BF=![]() BE,
BE,
∴DF=BD﹣BF=![]() AB﹣
AB﹣![]() BE=
BE=![]() (AB﹣BE)=
(AB﹣BE)=![]() AE,
AE,
∴![]() ,
,
故答案为:![]() ;
;
(2)DF=![]() AE,
AE,
理由:由(1)知,BF=![]() BE,BD=
BE,BD=![]() AB,∠BFE=∠ABD=45
AB,∠BFE=∠ABD=45![]() ,
,
∴![]() ,
,
由旋转知,∠ABE=∠DBF,
∴△ABE∽△DBF,
∴![]() ,
,
∴DF=![]() AE;
AE;
(3)如图3,连接DE,CE,
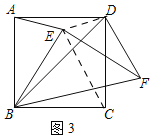
∵EA=ED,
∴点E在AD的中垂线上,
∴AE=DE,BE=CE,
∵四边形ABCD是正方形,
∴∠BAD=∠ABC=90![]() ,AB=BC,
,AB=BC,
∴BE=CE=BC,
∴△BCE是等边三角形,
∴∠CBE=60![]() ,
,
∴∠ABE=∠ABC-∠CBE=90![]() -60
-60![]() =30
=30![]() ,
,
即:α=30![]() ,
,
如图4,同理,△BCE是等边三角形,

∴∠ABE=∠ABC+∠CBE=90![]() +60
+60![]() =150
=150![]() ,
,
即:α=150![]() ,
,
故答案为:30![]() 或150
或150![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为做好全国文明城市的创建工作,我市交警连续![]() 天对某路口
天对某路口![]() 个“
个“![]() 岁以下行人”和
岁以下行人”和![]() 个“
个“![]() 岁及以上行人”中出现交通违章的情况进行了调查统计,将所得数据绘制成如下统计图.请根据所给信息,解答下列问题.
岁及以上行人”中出现交通违章的情况进行了调查统计,将所得数据绘制成如下统计图.请根据所给信息,解答下列问题.
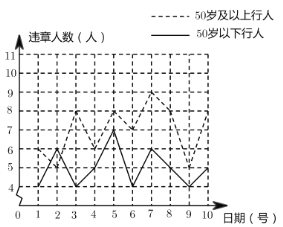
(1)求这![]() 天“
天“![]() 岁及以上行人”中每天违章人数的众数.
岁及以上行人”中每天违章人数的众数.
(2)某天中午下班时段经过这一路口的“![]() 岁以下行人”为
岁以下行人”为![]() 人,请估计大约有多少人会出现交通违章行为.
人,请估计大约有多少人会出现交通违章行为.
(3)请根据以上交通违章行为的调查统计,就文明城市创建减少交通违章提出合理建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且点C是弧AB的中点,若扇形的半径为![]() ,则图中阴影部分的面积等于_____.
,则图中阴影部分的面积等于_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有红、黄两个盒子,红盒子中藏有三张分别标有数字![]() ,
,![]() ,1的卡片,黄盒子中藏有三张分别标有数字1,3,2的卡片,卡片外形相同.现甲从红盒子中取出一张卡片,乙从黄盒子中取出一张卡片,并将它们的数字分别记为a,b.
,1的卡片,黄盒子中藏有三张分别标有数字1,3,2的卡片,卡片外形相同.现甲从红盒子中取出一张卡片,乙从黄盒子中取出一张卡片,并将它们的数字分别记为a,b.
(1)请你用树形图或列表法列出所有可能的结果.
(2)现制定这样一个游戏规则:若所选出的a,b能使得二次函数y=ax2+bx+1的图像与x轴有两个不同的交点,则称甲获胜;否则称乙获胜.请问这样的游戏规则公平吗?请你用概率知识解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了庆祝中华人民共和国成立70周年,某市决定开展“我和祖国共成长”主题演讲比赛,某中学将参加本校选拔赛的40名选手的成绩(满分为100分,得分为正整数且无满分,最低为75分)分成五组,并绘制了下列不完整的统计图表.
分数段 | 频数 | 频率 |
74.5~79.5 | 2 | 0.05 |
79.5~84.5 | m | 0.2 |
84.5~89.5 | 12 | 0.3 |
89.5~94.5 | 14 | n |
94.5~99.5 | 4 | 0.1 |
(1)表中m=__________,n=____________;
(2)请在图中补全频数直方图;
(3)甲同学的比赛成绩是40位参赛选手成绩的中位数,据此推测他的成绩落在_________分数段内;
(4)选拔赛中,成绩在94.5分以上的选手,男生和女生各占一半,学校从中随机确定2名选手参加全市决赛,请用列举法或树状图法求恰好是一名男生和一名女生的概率.
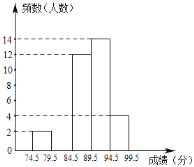
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是原点,
是原点,![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() .
.
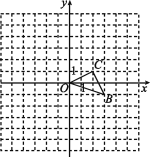
(1)以点![]() 为位似中心,在
为位似中心,在![]() 轴的左侧将
轴的左侧将![]() 扩大为原来的两倍(即新图与原图的相似比为
扩大为原来的两倍(即新图与原图的相似比为![]() ),画出图形,并写出点
),画出图形,并写出点![]() 的对应点的坐标;
的对应点的坐标;
(2)如果![]() 内部一点
内部一点![]() 的坐标为
的坐标为![]() ,写出点
,写出点![]() 的对应点
的对应点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com