
【题目】已知△ABC中, ![]() ,
, ![]() ,△CDE中,
,△CDE中, ![]() ,CD=DE=5,
,CD=DE=5,
连接接BE,取BE中点F,连接AF、DF.
(1)如图1,若![]() 三点共线,
三点共线, ![]() 为
为![]() 中点.
中点.
①直接指出![]() 与
与![]() 的关系______________;
的关系______________;
②直接指出![]() 的长度______________;
的长度______________;
(2)将图(1)中的△CDE绕![]() 点逆时针旋转
点逆时针旋转![]() (如图2,
(如图2, ![]() ),试确定
),试确定![]() 与
与![]() 的关系,并说明理由;
的关系,并说明理由;
(3)在(2)中,若![]() ,请直接指出点
,请直接指出点![]() 所经历的路径长.
所经历的路径长.


图1 图2
【答案】(1)①![]() ,
, ![]() ,②
,②![]() ;(2)
;(2)![]() ,
, ![]() ,理由见解析;(3)
,理由见解析;(3)![]() 或
或![]()
【解析】试题分析:(1)①如图,过点F M⊥CD于M,FN⊥AC交CA的延长线于点N,根据已知条件易证四边形FMCN为正方形,可得FN=FM,再证△FNA≌△FMD,即可得∠NFA=∠DFM,DF=AF,所以∠NFA+∠AFM=∠DFM+∠AFM=∠DFA=90°,即可证得![]() ;②根据勾股定理求得BC=
;②根据勾股定理求得BC=![]() ,EC=5
,EC=5![]() ,因
,因![]() 为
为![]() 中点,F为BE的中点,可得CH=BH=
中点,F为BE的中点,可得CH=BH=![]() ,EB=5
,EB=5![]() -
-![]() =
=![]() ,EF=BF=
,EF=BF=![]() ,所以FH=BF+BH=
,所以FH=BF+BH=![]() ;
;
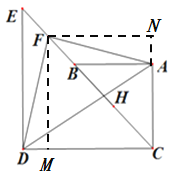
(2) ![]() ,
, ![]() ,延长
,延长![]() 至
至![]() 使
使![]() ,连接
,连接![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,
, ![]() ,
, ![]() ,
, ![]() ,再证得
,再证得![]() ,由
,由![]() ,CD=DE,根据SAS判定
,CD=DE,根据SAS判定![]() ,
, ![]() ,
, ![]() ,
, ![]() ,根据等腰直角三角形的性质可得
,根据等腰直角三角形的性质可得![]() ,
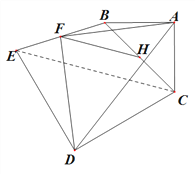
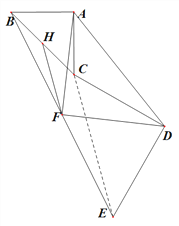
, ![]() ; (3)如图,当旋转
; (3)如图,当旋转![]() 或
或![]() 时,
时, ![]() ,AD=7,点
,AD=7,点![]() 经历的路径长为
经历的路径长为![]() 或
或![]() .
.
试题解析:
(1)(1)①![]() ,
, ![]()
②![]()
(2)结论: ![]() ,
, ![]() 理由如下:
理由如下:
延长![]() 至
至![]() 使
使![]() ,连接
,连接![]() ,延长
,延长![]() 交
交![]() 于
于![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]()
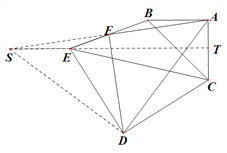
(3)旋转![]() 或
或![]() 时,
时, ![]() ,AD=7,点
,AD=7,点![]() 经历的路径长为
经历的路径长为![]() 或
或![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为了推进书香校园建设,加强学生课外阅读,某校开展了“走近名家名篇”的主题活动;学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频数分布表和频数分布直方图的一部分,如下:
时间(单位: | 频数(人数) | 频率 |
| 2 | 0.04 |
| 3 | 0.06 |
| 15 | 0.30 |
|
| 0.50 |
| 5 |
|

请根据图表信息回答下列问题:
(1)频数分布表中的![]() _________,
_________,![]() ___________;
___________;
(2)将频数分布直方图补充完整;
(3)学校将每周课外阅读时间在8小时以上的学生评为“阅读之星”,请你估计该校1200名学生中评为“阅读之星”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三张形状、大小相同但画面不同的风景图片,都按同样的方式剪成相同的三段,然后将上、中、下三段分别混合洗匀,从三堆图片中随机各抽出一张, 求这三张图片恰好组成一张完整风景图片的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表数据是科研小组在某地区根据调查获取的:“距离地面的高度(千米)与此处的温度(摄氏度)”的关系。
距离地面高度/千米 | 0 | 1 | 2 | 3 | 4 | 5 |
温度/摄氏度 | 20 | 14 | 8 | 2 | -4 | -10 |
根据上表,请你回答:
(1)上表中___________是自变量;_________________是因变量;
(2)如果用![]() 表示距离地面的高度(千米),
表示距离地面的高度(千米),![]() 表示温度(摄氏度),请你写出
表示温度(摄氏度),请你写出![]() 与
与![]() 的关系式____________________________________;
的关系式____________________________________;
(3)请你利用(2)的结论,求该地区:①距离地面6.2千米的高空温度是多少?②当高空某处温度为-52度时,该处的高度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知正方形ABCD和正方形AEFG有公共顶点A,连接BE,DG.


(1)问:BE与DG有什么关系?说明理由.
(2)如图2,已知AB=4,AE=![]() ,当点F在边AD上时,求BE的长.
,当点F在边AD上时,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com