
 如图所示,一根木棒AB长为2,斜靠在与地面OM垂直的墙壁ON上,与地面的倾斜角(∠ABO)为60°,当木棒A端沿NO向下滑动到A′,B端沿直线OM向右滑动到B′,若AA′=$\sqrt{3}$-1,则木棒的中点从P随之运动到P′所经过的路径长为$\frac{π}{6}$.
如图所示,一根木棒AB长为2,斜靠在与地面OM垂直的墙壁ON上,与地面的倾斜角(∠ABO)为60°,当木棒A端沿NO向下滑动到A′,B端沿直线OM向右滑动到B′,若AA′=$\sqrt{3}$-1,则木棒的中点从P随之运动到P′所经过的路径长为$\frac{π}{6}$. 分析 根据直角三角形斜边上的中线等于斜边的一半得到OP=$\frac{1}{2}$AB=$\frac{1}{2}$A′B′=OP′,即P是随之运动所经过的路线是一段圆弧;在Rt△AOB中,根据含30度的直角三角形三边的关系得到∠AOP=30°,OA=$\sqrt{3}$,则易求出OA′=OA-AA′=1,即可得到△A′OB′为等腰直角三角形,得到∠A′B′O=45°,则∠POP′=∠A′OP′-∠AOP=15°,然后根据弧长公式计算即可.
解答 解:如图,连接OP、OP′,
∵ON⊥OM,P为AB中点,
∴OP=$\frac{1}{2}$AB=$\frac{1}{2}$A′B′=OP′,
∵AB=2,
∴OP=1,
当A端下滑B端右滑时,AB的中点P到O的距离始终为定长1,
∴P是随之运动所经过的路线是一段圆弧,
∵∠ABO=60°,
∴∠AOP=30°,OA=$\sqrt{3}$,
∵AA′=$\sqrt{3}$-1,OA′=OA-AA′=1,
∴sin∠A′B′O=$\frac{OA′}{A′B′}$=$\frac{1}{2}$,
∴∠A′B′O=45°,
∴∠A′OP=45°
∴∠POP′=∠A′OP′-∠AOP=15°,
∴弧PP′的长=$\frac{15π×\frac{1}{2}}{180}$=$\frac{π}{6}$,
即P点运动到P′所经过路线PP′的长为$\frac{π}{6}$,
故答案是:$\frac{π}{6}$.
点评 本题考查了轨迹和弧长公式:l=$\frac{nπR}{180}$(n为弧所对的圆心角的度数,R为半径),也考查了直角三角形斜边上的中线等于斜边的一半以及含30度的直角三角形三边的关系和等腰直角三角形的性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 如图,点P是∠AOB的角平分线上的一点,过点P作PC∥OA交OB于点C,PD⊥OA,若∠AOB=60°,OC=6,则PD=3$\sqrt{3}$.
如图,点P是∠AOB的角平分线上的一点,过点P作PC∥OA交OB于点C,PD⊥OA,若∠AOB=60°,OC=6,则PD=3$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
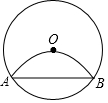 如图,线段AB是⊙O的弦,点P在⊙O上(点P不与点A、点B重合),连接AP、BP,若将⊙O沿弦AB折叠,圆弧恰好经过圆心O,则∠APB的大小为60°或120度.
如图,线段AB是⊙O的弦,点P在⊙O上(点P不与点A、点B重合),连接AP、BP,若将⊙O沿弦AB折叠,圆弧恰好经过圆心O,则∠APB的大小为60°或120度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com