
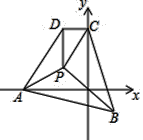
【题目】如图,在平面直角坐标系中,已知四个定点![]() 、
、![]() 、
、![]() 、
、![]() ,点
,点![]() 在四边形
在四边形![]() 内,则到四边形四个顶点的距离的和
内,则到四边形四个顶点的距离的和![]() 最小时的点
最小时的点![]() 的坐标为______.
的坐标为______.
【答案】(-![]() ,
,![]() )
)
【解析】
设AC与BD交于P′点,则由不等式的性质可得,PA+PC≥AC=P′A+P′C,PB+PD≥BD=P′B+P′D,得出PA+PB+PC+PD≥AC+BD,所以当P在P′处时PA+PB+PC+PD的值最小,再根据点P′为直线AC与BD的交点可求出此时点P′的坐标.
解:如图,设AC与BD交于P′点,则PA+PC≥AC=P′A+P′C,PB+PD≥BD=P′B+P′D,

因此,PA+PB+PC+PD≥AC+BD,当动点P在P′的位置时,PA+PB+PC+PD的值最小,
设直线AC的解析式为y=kx+b,将点A(-3,0),C(0,3)代入得,
![]() ,解得
,解得![]() ,∴直线AC的解析式为y=x+3①,
,∴直线AC的解析式为y=x+3①,
同理根据点B(1,-1),D(-1,3)可得直线BD的解析式为y=-2x+1②,
联立①②得,![]() ,解得
,解得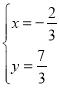 .
.
∴此时点P的坐标为:![]() .
.
故答案为:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:①a﹣b+c>0;②3a+b=0;③b2=4a(c﹣n);④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.其中正确结论的是______________(只填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的点
中的点![]() 和
和![]() (半径为
(半径为![]() ),给出如下定义:若点
),给出如下定义:若点![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,且
,且![]() ,则称点
,则称点![]() 为
为![]() 的称心点.
的称心点.
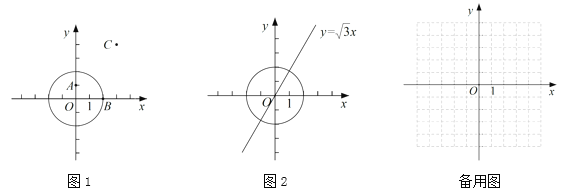
(1)当![]() 的半径为2时,
的半径为2时,
①如图1,在点![]() ,
,![]() ,
,![]() 中,
中,![]() 的称心点是 ;
的称心点是 ;
②如图2,点![]() 在直线
在直线![]() 上,若点
上,若点![]() 是
是![]() 的称心点,求点
的称心点,求点![]() 的横坐标
的横坐标![]() 的取值范围;
的取值范围;
(2)![]() 的圆心为
的圆心为![]() ,半径为2,直线
,半径为2,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() .若线段
.若线段![]() 上的所有点都是
上的所有点都是![]() 的称心点,直接写出
的称心点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,P是边BC上的一动点(不与点B,C重合),点B关于直线AP的对称点为E,连接AE,连接DE并延长交射线AP于点F,连接BF
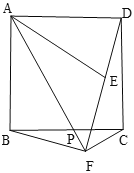
(1)若![]() ,直接写出
,直接写出![]() 的大小(用含
的大小(用含![]() 的式子表示).
的式子表示).
(2)求证:![]() .
.
(3)连接CF,用等式表示线段AF,BF,CF之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现今“微信运动”被越来越多的人关注和喜爱,某数学兴趣小组随机调查了我市![]() 名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

请根据以上信息,解答下列问题:
(1)写出![]() ,
,![]() ,
,![]() ,
,![]() 的值并补全频数分布直方图;
的值并补全频数分布直方图;
(2)我市约有![]() 名教师,用调查的样本数据估计日行走步数超过
名教师,用调查的样本数据估计日行走步数超过![]() 步(包含
步(包含![]() 步)的教师有多少名?
步)的教师有多少名?
(3)若在![]() 名被调查的教师中,选取日行走步数超过
名被调查的教师中,选取日行走步数超过![]() 步(包含
步(包含![]() 步)的两名教师与大家分享心得,用树形图或列表法求被选取的两名教师恰好都在
步)的两名教师与大家分享心得,用树形图或列表法求被选取的两名教师恰好都在![]() 步(包含
步(包含![]() 步)以上的概率.
步)以上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
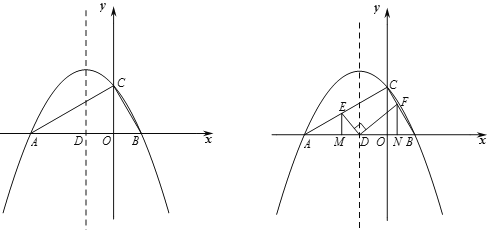
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 点在
点在![]() 点的左侧),与
点的左侧),与![]() 轴交于点
轴交于点![]() ,抛物线的对称轴与
,抛物线的对称轴与![]() 轴交于点
轴交于点![]() .
.
(1)请直接写出![]() 、
、![]() 两点的坐标及
两点的坐标及![]() 的度数;
的度数;
(2)如图1,若点![]() 为抛物线对称轴上的点,且
为抛物线对称轴上的点,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图![]() ,若点
,若点![]() 、
、![]() 分别为线段
分别为线段![]() 和
和![]() 上的动点,且
上的动点,且![]() ,过
,过![]() 、
、![]() 分别作
分别作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() 、
、![]() .在
.在![]() 、
、![]() 两点的运动过程中,试探究:
两点的运动过程中,试探究:
①![]() 是否是一个定值?如果是,请求出这个定值,如果不是,请说明理由;
是否是一个定值?如果是,请求出这个定值,如果不是,请说明理由;
②若将![]() 沿着
沿着![]() 翻折得到
翻折得到![]() ,将
,将![]() 沿着
沿着![]() 翻折得到
翻折得到![]() ,当点
,当点![]() 从点
从点![]() 运动到点
运动到点![]() 的过程中,求点
的过程中,求点![]() 和点
和点![]() 的运动轨迹的长度之和.
的运动轨迹的长度之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了帮助市内一名患“白血病”的中学生,东营市某学校数学社团15名同学积极捐款,捐款情况如下表所示,下列说法正确的是( )
捐款数额 | 10 | 20 | 30 | 50 | 100 |
人数 | 2 | 4 | 5 | 3 | 1 |
A. 众数是100 B. 中位数是30 C. 极差是20 D. 平均数是30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开展阳光体育运动,掌握运动技能,增强身体素质.某校初二年级五月开展了周末一小时兴趣锻炼活动,项目包括:篮球技能、排球技能、足球技能、立定跳远、50米跑,每个同学只选一项参与.王老师为了解学生对各种项目的参与情况,随机调查了部分学生参与哪一类项目(被调查的学生没有不参与的),并将调查结果制成了如下的两个统计图(不完整)请你根据图中所提供的信息,完成下列问题:
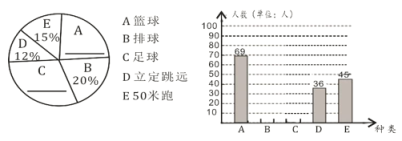
(1)求本次调查的学生人数;
(2)请将两个统计图补充完整,并求出足球项目在扇形统计图中所占圆心角的度数;
(3)若该中学初二年级有![]() 名学生,请估计该校初二学生参与球类项目的人数.
名学生,请估计该校初二学生参与球类项目的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
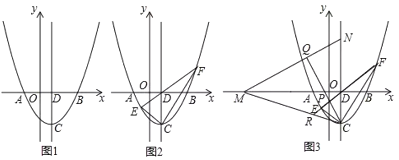
【题目】平面直角坐标系中,![]() 是坐标原点,抛物线
是坐标原点,抛物线![]() 交
交![]() 轴于
轴于![]() 两点(如图),顶点是
两点(如图),顶点是![]() ,对称轴交
,对称轴交![]() 轴于点
轴于点![]()
(1)如图(1)求抛物线的解析式;
(2)如图(2)![]() 是第三象限抛物线上一点,连接
是第三象限抛物线上一点,连接![]() 并延长交抛物线于点
并延长交抛物线于点![]() ,连接
,连接![]() 求证:
求证:![]() ;
;
(3)如图(3)在(2)问条件下,![]() 分别是线段
分别是线段![]() 延长线上一点,连接
延长线上一点,连接![]() ,过点
,过点![]() 作
作![]() 于
于![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,若
,若![]()
![]()
![]() 求点
求点![]() 坐标.
坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com