
如图,抛物线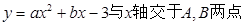 ,与
,与 轴交于点
轴交于点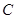 ,且
,且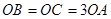 .
.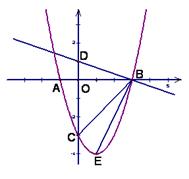
【小题1】(1)求抛物线的解析式;
【小题2】(2)探究坐标轴上是否存在点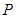 ,使得以点
,使得以点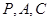 为顶点的三角形为直角三角形?
为顶点的三角形为直角三角形?
若存在,求出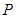 点坐标,若不存在,请说明理由;
点坐标,若不存在,请说明理由;
【小题3】(3)直线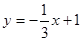 交
交 轴于
轴于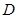 点,
点,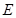 为抛物线顶点.若
为抛物线顶点.若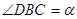 ,
,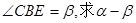 的值.
的值.
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
如图,抛物线:![]() 与
与![]() 轴交于点A(-2,0)和B(4,0)、与
轴交于点A(-2,0)和B(4,0)、与![]() 轴交于点C.
轴交于点C.
(1)求抛物线的解析式;
(2![]() )T是抛物线对称轴上的一点,且△ACT是以AC为底的等腰三角形,求点T的坐标;
)T是抛物线对称轴上的一点,且△ACT是以AC为底的等腰三角形,求点T的坐标;
(3)点M、Q分别从点A、B以每秒1个单位长度的速度沿![]() 轴同时出发相向而行.当点M到原点时,点Q立刻掉头并以每秒
轴同时出发相向而行.当点M到原点时,点Q立刻掉头并以每秒![]() 个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动.过点M的直线l⊥轴,交AC或BC于点P.求点M的运动时间t(秒)与△APQ的面积S的函数关系式,并求出S的最大值.
个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动.过点M的直线l⊥轴,交AC或BC于点P.求点M的运动时间t(秒)与△APQ的面积S的函数关系式,并求出S的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,抛物线![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() .
.
1.(1)求抛物线的解析式;
2.(2)探究坐标轴上是否存在点![]() ,使得以点
,使得以点![]() 为顶点的三角形为直角三角形?
为顶点的三角形为直角三角形?
若存在,求出![]() 点坐标,若不存在,请说明理由;
点坐标,若不存在,请说明理由;
3.(3)直线![]() 交
交![]() 轴于
轴于![]() 点,
点,![]() 为抛物线顶点.若
为抛物线顶点.若![]() ,
,
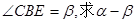 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
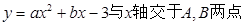 ,与
,与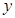 轴交于点
轴交于点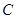 ,且
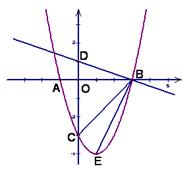
,且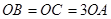 .
.
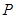 ,使得以点
,使得以点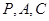 为顶点的三角形为直角三角形?
为顶点的三角形为直角三角形?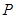 点坐标,若不存在,请说明理由;
点坐标,若不存在,请说明理由;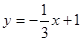 交
交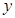 轴于
轴于 点,
点,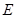 为抛物线顶点.若
为抛物线顶点.若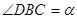 ,
,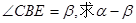 的值.
的值.查看答案和解析>>
科目:初中数学 来源:2011-2012年北京育才学校九年级第一学期期中考试数学卷 题型:解答题
如图,抛物线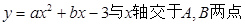 ,与
,与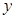 轴交于点
轴交于点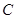 ,且
,且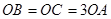 .
.
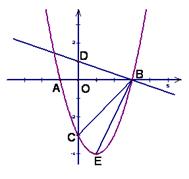
1.(1)求抛物线的解析式;
2.(2)探究坐标轴上是否存在点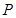 ,使得以点
,使得以点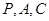 为顶点的三角形为直角三角形?
为顶点的三角形为直角三角形?
若存在,求出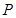 点坐标,若不存在,请说明理由;
点坐标,若不存在,请说明理由;
3.(3)直线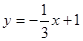 交
交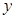 轴于
轴于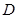 点,
点,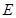 为抛物线顶点.若
为抛物线顶点.若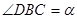 ,
,
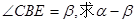 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com