
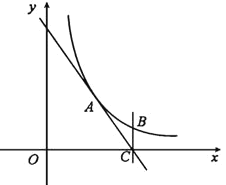
【题目】如图,反比例函数![]() 过点
过点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() 过点
过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交反比例函数图象于点
交反比例函数图象于点![]() .
.
(1)求![]() 的值与
的值与![]() 点的坐标;
点的坐标;
(2)连结![]() ,求
,求![]() 的面积;
的面积;
(3)在平面内有点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() ,
,![]() 四点为顶点的四边形为平行四边形,试写出符合条件的所有
四点为顶点的四边形为平行四边形,试写出符合条件的所有![]() 点的坐标.
点的坐标.
【答案】(1)![]() ;
;![]() ;(2)3;(3)
;(2)3;(3)![]() .
.
【解析】
(1)将A点的坐标代入反比例函数![]() 求得k的值,然后将x=6代入反比例函数解析式求得相应的y的值,即得点B的坐标;
求得k的值,然后将x=6代入反比例函数解析式求得相应的y的值,即得点B的坐标;
(2)利用三角形面积公式解答即可;
(3)使得以A、B、C、D为顶点的四边形为平行四边形,如图所示,求出满足题意的D的坐标即可.
(1)∵点![]() 在反比例函数
在反比例函数![]() 的图象上,
的图象上,
∴![]()
∴![]()
∵![]() 轴,
轴,![]()
∴点![]() 的横坐标为6.
的横坐标为6.
又∵点![]() 在
在![]() 的图象上,
的图象上,
∴![]()
∴![]() ;
;
(2)∵![]() 到
到![]() 的距离为3.
的距离为3.
又∵![]()
∴![]() ;
;
(3) ①如图,当四边形ABCD为平行四边形时,AD∥BC且AD=BC.
∵A(3,4)、B(6,2)、C(6,0),
∴点D的横坐标为3,yAyD=yByC即4yD=20,故yD=2.
所以D(3,2).
②如图,当四边形ACBD′为平行四边形时,AD′∥CB且AD′=CB.
∵A(3,4)、B(6,2)、C(6,0),
∴点D的横坐标为3,yD′yA=yByC即yD′4=20,故yD′=6.
所以D′(3,6).
③如图,当四边形ACD″B为平行四边形时,AC=BD″且AC∥BD″.
∵A(3,4)、B(6,2)、C(6,0),
∴xD″xB=xCxA即xD″6=63,故xD″=9.
yD″yB=yCyA即yD″2=04,故yD″=2.
所以D″(9,2).
综上所述,符合条件的点D的坐标是:(3,2)或(3,6)或(9,2).


科目:初中数学 来源: 题型:
【题目】由于各地雾霾天气越来越严重,2018年春节前夕,安庆市政府号召市民,禁放烟花炮竹.学校向3000名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:使用电子鞭炮;D类:不会减少烟花爆竹数量”四个选项进行问卷调查(单选),并将对100名学生的调查结果绘制成统计图(如图所示).根据抽样结果,请估计全校“使用电子鞭炮”的学生有( )
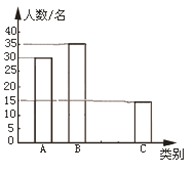
A. 900名 B. 1050名 C. 600名 D. 450名
【答案】D
【解析】分析:用全校学生的人数乘以“使用电子鞭炮”的百分比即可求出答案.
详解:100名学生中“使用电子鞭炮”的学生有![]() 人,“使用电子鞭炮”的百分比为:
人,“使用电子鞭炮”的百分比为:![]()
全校“使用电子鞭炮”的学生有:![]() 人.
人.
故选D.
点睛:考查用样本估计总体,从条形统计图中得到“使用电子鞭炮”的学生人数是解题的关键.
【题型】单选题
【结束】
9
【题目】如图,在□ABCD中,E、F分别为BC、AD的中点,AE、CF分别交BD于点M、N,则四边形 AMCN与□ABCD的面积比为( )
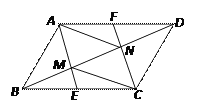
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
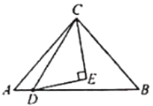
【题目】如图,在等腰直角![]() 中,
中,![]() ,
,![]() ,D是AB上一个动点,以DC为斜边作等腰直角
,D是AB上一个动点,以DC为斜边作等腰直角![]() ,使点E和A位于CD两侧。点D从点A到点B的运动过程中,
,使点E和A位于CD两侧。点D从点A到点B的运动过程中,![]() 周长的最小值是________.
周长的最小值是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,反比例函数![]() 的图象过第二象限内的点
的图象过第二象限内的点![]() ,
,![]() 轴于
轴于![]() ,
,![]() 面积为3,若直线
面积为3,若直线![]() 经过点
经过点![]() ,并且经过反比例函数
,并且经过反比例函数![]() 的图象上另一点
的图象上另一点![]() .
.
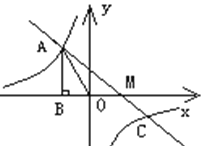
(1)求反比例函数的解析式;
(2)求直线![]() 解析式
解析式
(3)求![]() 的面积;
的面积;
(4)直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知线段![]() ,
,![]() ,线段
,线段![]() 在线段
在线段![]() 上运动,
上运动,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.
![]()
(1)若![]() ,则
,则![]() ______
______![]() ;
;
(2)当线段![]() 在线段
在线段![]() 上运动时,试判断
上运动时,试判断![]() 的长度是否发生变化?如果不变请求出
的长度是否发生变化?如果不变请求出![]() 的长度,如果变化,请说明理由;
的长度,如果变化,请说明理由;
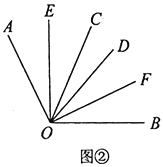
(3)我们发现角的很多规律和线段一样,如图②已知![]() 在
在![]() 内部转动,
内部转动,![]() 、
、![]() 分别平分
分别平分![]() 和
和![]() ,则
,则![]() 、
、![]() 和
和![]() 有何数量关系,请直接写出结果不需证明.
有何数量关系,请直接写出结果不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了开发利用海洋资源,某勘测飞机预测量一岛屿两端A、B的距离,飞机在距海平面垂直高度为100米的点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500米,在点D测得端点B的俯角为45°,求岛屿两端A、B的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是关于x的一元二次方程
是关于x的一元二次方程![]() 的两个实数根.
的两个实数根.
(1)是否存在实数k,使![]() 成立?若存在,求出k的值;若不存在,请说明理由.
成立?若存在,求出k的值;若不存在,请说明理由.
(2)求使![]() 的值为整数的实数k的整数值.
的值为整数的实数k的整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A.篮球 B.乒乓球C.羽毛球 D.足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,

请回答下列问题:
(1)这次被调查的学生共有多少人?
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com