
【题目】如图,已知抛物线y=﹣x2+bx+c经过A(3,0),B(0,3)两点.
(1)求此抛物线的解析式和直线AB的解析式;
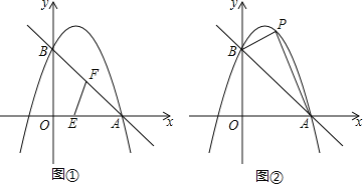
(2)如图①,动点E从O点出发,沿着OA方 向 以1个单位/秒的速度向终点A匀速运动,同时, 动点F从A点出发,沿着AB方向以![]() 个单位/ 秒的速度向终点B匀速运动,当E,F中任意一点到达终点时另一点也随之停止运动,连接EF,设运动时间为t秒,当t为何值时,△AEF为直角三角形?
个单位/ 秒的速度向终点B匀速运动,当E,F中任意一点到达终点时另一点也随之停止运动,连接EF,设运动时间为t秒,当t为何值时,△AEF为直角三角形?
(3)如图②,取一根橡皮筋,两端点分别固定在A,B处,用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P与A,B两点构成无数个三角形,在这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时点P的坐标;如果不存在,请简要说明理由.
【答案】(1)抛物线的解析式为y=﹣x2+2x+3,直线AB的解析式为y=﹣x+3;(2)t=![]() 或
或![]() ;(3)存在面积最大,最大值是
;(3)存在面积最大,最大值是![]() ,此时点P(
,此时点P(![]() ,
,![]() ).
).
【解析】
(1)将A(3,0),B(0,3)两点代入y=﹣x2+bx+c,求出b及c即可得到抛物线的解析式,设直线AB的解析式为y=kx+n,将A、B两点坐标代入即可求出解析式;
(2)由题意得OE=t,AF=![]() t,AE=OA﹣OE=3﹣t,分两种情况:①若∠AEF=∠AOB=90°时,证明△AOB∽△AEF得到
t,AE=OA﹣OE=3﹣t,分两种情况:①若∠AEF=∠AOB=90°时,证明△AOB∽△AEF得到![]() =
=![]() ,求出t值;②若∠AFE∠AOB=90°时,证明△AOB∽△AFE,得到
,求出t值;②若∠AFE∠AOB=90°时,证明△AOB∽△AFE,得到![]() =
=![]() 求出t的值;
求出t的值;
(3)如图,存在,连接OP,设点P的坐标为(x,﹣x2+2x+3),根据![]() ,得到
,得到![]() ,由此得到当x=
,由此得到当x=![]() 时△ABP的面积有最大值,最大值是
时△ABP的面积有最大值,最大值是![]() ,并求出点P的坐标.
,并求出点P的坐标.
(1)∵抛物线y=﹣x2+bx+c经过A(3,0),B(0,3)两点,
∴![]() ,解得
,解得![]() ,
,
∴抛物线的解析式为y=﹣x2+2x+3,
设直线AB的解析式为y=kx+n,
∴ ![]() ,解得
,解得![]() ,
,
∴直线AB的解析式为y=﹣x+3;
(2)由题意得,OE=t,AF=![]() t,
t,
∴AE=OA﹣OE=3﹣t,
∵△AEF为直角三角形,
∴①若∠AEF=∠AOB=90°时,
∵∠BAO=∠EAF,
∴△AOB∽△AEF
∴![]() =
=![]() ,
,
∴![]() ,
,
∴t=![]() .
.
②若∠AFE∠AOB=90°时,
∵∠BAO=∠EAF,
∴△AOB∽△AFE,
∴![]() =
=![]() ,
,
∴![]() ,
,
∴t=![]() ;
;
综上所述,t=![]() 或
或![]() ;
;
(3)如图,存在,
连接OP,设点P的坐标为(x,﹣x2+2x+3),
∵![]() ,
,
∴![]()
=![]()
=![]()
=![]() ,
,
∵![]() <0,
<0,
∴当x=![]() 时△ABP的面积有最大值,最大值是
时△ABP的面积有最大值,最大值是![]() ,
,
此时点P(![]() ,
,![]() ).
).



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.
(1)求两个路灯之间的距离;
(2)当小华走到路灯B的底部时,他在路灯A下的影长是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2![]() cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“大美湿地,水韵盐城”.某校数学兴趣小组就“最想去的盐城市旅游景点”随机调查了本校部分学生,要求每位同学选择且只能选择一个最想去的景点,下面是根据调查结果进行数据整理后绘制出的不完整的统计图:

请根据图中提供的信息,解答下列问题:
(1)求被调查的学生总人数;
(2)补全条形统计图,并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数;
(3)若该校共有800名学生,请估计“最想去景点B“的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
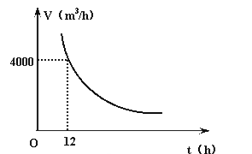
【题目】如图所示是某一蓄水池每小时的排水量V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图象.
(1)请你根据图象提供的信息求出此蓄水池的总蓄水量;
(2)写出此函数的解析式;
(3)若要6 h排完水池中的水,那么每小时的排水量应该是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解放桥是天津市的标志性建筑之一,是一座全钢结构的部分可开启的桥梁,
(I)如图①,已知解放桥可开启部分的桥面的跨度AB等于47m,从AB的中点C处开启,则AC开启至A'C'的位置时,A'C'的长为 .
(II)如图②,某校数学兴趣小组要测量解放桥的全长PQ,在观景平台M处测得∠PMQ=54°,沿河岸MQ前行,在观景平台N处测得∠PNQ=73°。已知PQ⊥MQ,MN=40m,求解放桥的全长PQ(tan54°≈1.4,tan73°≈3.3,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雾霾天气给人们的生活带来很大影响,空气质量问题备受人们关注,为了减少雾霾影响,某单位计划为职工购买![]() 、
、![]() 两种型号的防霾口罩.已知每个
两种型号的防霾口罩.已知每个![]() 种型号防霾口罩价格比每个
种型号防霾口罩价格比每个![]() 种型号防霾口罩价格多
种型号防霾口罩价格多![]() 元,花
元,花![]() 元购买
元购买![]() 种型号防霾口罩和花
种型号防霾口罩和花![]() 元购买
元购买![]() 种型号防霾口罩的数量相同.
种型号防霾口罩的数量相同.
(1)求![]() 、
、![]() 两种型号防霾口罩每个价格各多少元?
两种型号防霾口罩每个价格各多少元?
(2)根据单位实际情况,需购买![]() 、
、![]() 两种型号防霾口罩共
两种型号防霾口罩共![]() 个,总费用不高于
个,总费用不高于![]() 万元,求
万元,求![]() 种型号防霾口罩至少要购买多少个?
种型号防霾口罩至少要购买多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.
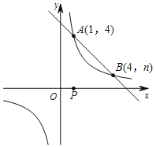
(1)求反比例函数和一次函数的解析式;
(2)直接写出当x>0时,![]() 的解集.
的解集.
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,延长AC到E,使CE=CO,连接EB,ED.
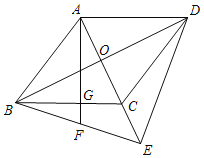
(1)求证:EB=ED;
(2)过点A作AF⊥AD,交BC于点G,交BE于点F,若∠AEB=45°,
①试判断△ABF的形状,并加以证明;
②设CE=m,求EF的长(用含m的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com