
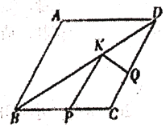
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() ,
,![]() 上的任意一点,则
上的任意一点,则![]() 的最小值为__________.
的最小值为__________.
【答案】![]()
【解析】
根据菱形的对称性,在AB上找到点P关于BD的对称点![]() ,过点
,过点![]() 作
作![]() Q⊥CD于Q,交BD于点K,连接PK,过点A作AE⊥CD于E,根据垂线段最短和平行线之间的距离处处相等,可得此时
Q⊥CD于Q,交BD于点K,连接PK,过点A作AE⊥CD于E,根据垂线段最短和平行线之间的距离处处相等,可得此时![]() 最小,且最小值为
最小,且最小值为![]() 的长,
的长,![]() ,然后利用锐角三角函数求AE即可.
,然后利用锐角三角函数求AE即可.
解:根据菱形的对称性,在AB上找到点P关于BD的对称点![]() ,过点
,过点![]() 作
作![]() Q⊥CD于Q,交BD于点K,连接PK,过点A作AE⊥CD于E
Q⊥CD于Q,交BD于点K,连接PK,过点A作AE⊥CD于E
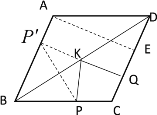
根据对称性可知:PK=![]() K,
K,
∴此时![]() =
=![]() ,根据垂线段最短和平行线之间的距离处处相等,
,根据垂线段最短和平行线之间的距离处处相等,
∴此时![]() 最小,且最小值为
最小,且最小值为![]() 的长,
的长,![]()
∵在菱形![]() 中,
中,![]() ,
,![]()
∴![]() ,∠ADE=180°-∠A=60°
,∠ADE=180°-∠A=60°
在Rt△ADE中,AE=AD·sin∠ADE=![]()
∴![]()
即![]() 的最小值为
的最小值为![]()
故答案为![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,AB=AC,以AB为直径作⊙O,分别交BC于点D,交CA的延长线于点E,过点D作
中,AB=AC,以AB为直径作⊙O,分别交BC于点D,交CA的延长线于点E,过点D作![]() 于点H,连接DE交线段OA于点F.
于点H,连接DE交线段OA于点F.
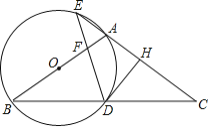
(1)试猜想直线DH与⊙O的位置关系,并说明理由;
(2)若AE=AH,EF=4,求DF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.
(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为 ;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解).

查看答案和解析>>
科目:初中数学 来源: 题型:
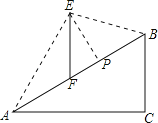
【题目】如图,在坡度i=1:![]() 的斜坡AB上立有一电线杆EF,工程师在点A处测得E的仰角为60°,沿斜坡前进20米到达B,此时测得点E的仰角为15°,现要在斜坡AB上找一点P,在P处安装一根拉绳PE来固定电线杆,以使EF保持竖直,为使拉绳PE最短,则FP的长度约为_____.(参考数据:
的斜坡AB上立有一电线杆EF,工程师在点A处测得E的仰角为60°,沿斜坡前进20米到达B,此时测得点E的仰角为15°,现要在斜坡AB上找一点P,在P处安装一根拉绳PE来固定电线杆,以使EF保持竖直,为使拉绳PE最短,则FP的长度约为_____.(参考数据:![]() =1.414,
=1.414,![]() =1.732)
=1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,双曲线y=![]() (k≠0)与直线y=ax+b(a≠0)交于A,B两点,直线AB分别交x轴,y轴于C、D两点,若OA=OC,A点坐标为(4,3).
(k≠0)与直线y=ax+b(a≠0)交于A,B两点,直线AB分别交x轴,y轴于C、D两点,若OA=OC,A点坐标为(4,3).
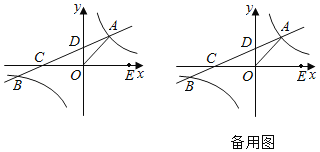
(1)分别求出双曲线与直线的函数表达式;
(2)若P为双曲线上一点,且横坐标为2,H为直线AB上一点,且PH+![]() HC最小,延长PH交x轴于点E,将线段OE沿x轴平移得线段O'E',在平移过程中,是否存在某个位置使|BO'﹣AE'|的值最大值,求出最大值并求出此时E点坐标.
HC最小,延长PH交x轴于点E,将线段OE沿x轴平移得线段O'E',在平移过程中,是否存在某个位置使|BO'﹣AE'|的值最大值,求出最大值并求出此时E点坐标.
(3)在(2)的情况下,将直线OA沿线段CE平移,平移过程中交y=![]() (x>0)的图象于M(M与点A不重合)交x轴于点N,在平面内找一点G,使M、N,E,G为顶点的四边形为矩形?直接写出G的坐标.
(x>0)的图象于M(M与点A不重合)交x轴于点N,在平面内找一点G,使M、N,E,G为顶点的四边形为矩形?直接写出G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
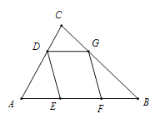
【题目】如图,在![]() 中,
中,![]() ,AB=5,BC=4,点D为边AC上的动点,作菱形DEFG,使点E、F在边AB上,点G在边BC上.若这样的菱形能作出两个,则AD的取值范围是( )
,AB=5,BC=4,点D为边AC上的动点,作菱形DEFG,使点E、F在边AB上,点G在边BC上.若这样的菱形能作出两个,则AD的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】岳阳市整治农村“空心房”新模式,获评全国改革开放40年地方改革创新40案例.据了解,我市某地区对辖区内“空心房”进行整治,腾退土地1200公顷用于复耕和改造,其中复耕土地面积比改造土地面积多600公顷.
(1)求复耕土地和改造土地面积各为多少公顷;
(2)该地区对需改造的土地进行合理规划,因地制宜建设若干花卉园和休闲小广场,要求休闲小广场总面积不超过花卉园总面积的![]() ,求休闲小广场的总面积最多为多少公顷.
,求休闲小广场的总面积最多为多少公顷.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF,若∠AOF=40°,则∠F的度数是( )
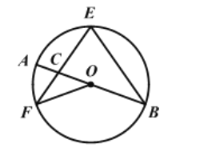
A.20°B.35°C.40°D.55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .
.
(1)如图1,若点![]() 是直线
是直线![]() 上方抛物线上的一个动点,过点
上方抛物线上的一个动点,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,点
,点![]() 为直线
为直线![]() 上一动点,点
上一动点,点![]() 为
为![]() 轴上一动点,连接
轴上一动点,连接![]() ,
,![]() .当
.当![]() 最长时,求
最长时,求![]() 的最小值;
的最小值;
(2)如图2,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得
得![]() ,将
,将![]() 沿直线
沿直线![]() 平移得到
平移得到![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,将
,将![]() 沿边
沿边![]() 翻折得
翻折得![]() ,连接
,连接![]() ,
,![]() ,当
,当![]() 是等腰三角形时,求此时点
是等腰三角形时,求此时点![]() 的坐标.
的坐标.
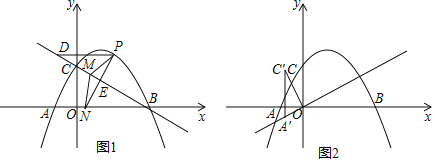
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com