
【题目】如图1,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .
.
(1)如图1,若点![]() 是直线
是直线![]() 上方抛物线上的一个动点,过点
上方抛物线上的一个动点,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,点
,点![]() 为直线
为直线![]() 上一动点,点
上一动点,点![]() 为
为![]() 轴上一动点,连接
轴上一动点,连接![]() ,
,![]() .当
.当![]() 最长时,求
最长时,求![]() 的最小值;
的最小值;
(2)如图2,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得
得![]() ,将
,将![]() 沿直线
沿直线![]() 平移得到
平移得到![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,将
,将![]() 沿边
沿边![]() 翻折得
翻折得![]() ,连接
,连接![]() ,
,![]() ,当
,当![]() 是等腰三角形时,求此时点
是等腰三角形时,求此时点![]() 的坐标.
的坐标.
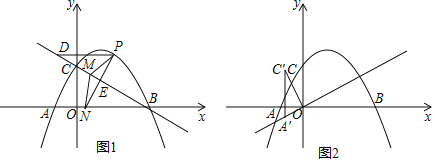
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)先求出A、B、C的坐标,直线BC解析式,可推出![]() ,设
,设![]() ,则
,则![]() ,推出
,推出![]() 时
时![]() 取得最大值,此时
取得最大值,此时![]() 最长,作直线
最长,作直线![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() ,交
,交![]() 轴于
轴于![]() ,将
,将![]() 转化为PK即可求值;
转化为PK即可求值;
(2)设![]() ,则
,则![]() ,
,![]() ,分别表示出
,分别表示出![]() ,
,![]() ,
,![]() ,再分别讨论两边相等,建立方程求解.
,再分别讨论两边相等,建立方程求解.
(1)令![]() ,得
,得![]() 或4,
或4,
令![]() 得
得![]()
∴![]() ,
,![]() ,
,![]()
BC=![]()
设直线BC解析式为:![]() ,代入
,代入![]() ,
,![]() 得:
得:
![]() ,解得
,解得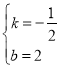
∴直线BC解析式为![]()
∵![]() ,
,![]() 轴,
轴,
∴∠PDE=∠CBO
∵∠PED=∠COB=90°
∴△PDE∽△CBO
∴![]()
∴![]() ,当
,当![]() 取得最大值时,线段
取得最大值时,线段![]() 最长.
最长.
设![]() ,则
,则![]()
∴![]()
∵![]()
∴当![]() ,即
,即![]() 时
时![]() 取得最大值,此时
取得最大值,此时![]() 最长
最长
作直线![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() ,交
,交![]() 轴于
轴于![]() ,与y轴交于F,
,与y轴交于F,
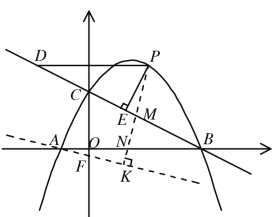
易得F点坐标为![]() ,
,
∴
∵∠OAF=∠KAN,∠AOF=∠AKN=90°
∴△AOF∽△AKN
∴![]() ,则
,则![]()
此时![]() ,
,
PK的长即为![]() 的最小值,
的最小值,
∵![]()
∴设直线PK的解析式为![]() ,将
,将![]() 代入得:
代入得:
![]() ,解得
,解得![]() ,即直线PK解析式为
,即直线PK解析式为![]()
联立![]() 与
与![]() 得:
得:
解得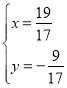 ,则M坐标为
,则M坐标为![]()
∴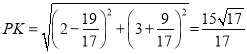
即![]() 的最小值为
的最小值为![]() .
.
(2)设![]() ,则
,则![]() ,
,![]()

∵![]()
∴![]()
![]()
![]()
当![]() 时,
时,![]() ,
,![]() 或
或![]()
当![]() 时,
时,![]() ,
,![]()
当![]() 时,
时,![]() ,
,![]()
∴![]() 或
或![]() 或
或![]()
∴![]() 或
或![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象和反比例函数
的图象和反比例函数![]() 的图象相交于
的图象相交于![]() 两点.
两点.

(1)试确定一次函数与反比例函数的解析式;
(2)求![]() 的面积;
的面积;
(3)结合图象,直接写出使![]() 成立的
成立的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
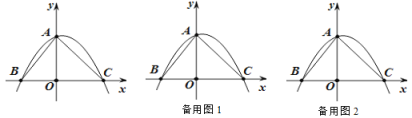
【题目】如图,抛物线y=ax2+bx+4(a≠0)与![]() 轴交于点B (-3 ,0) 和C (4 ,0)与
轴交于点B (-3 ,0) 和C (4 ,0)与![]() 轴交于点A.
轴交于点A.
(1) a = ,b = ;
(2) 点M从点A出发以每秒1个单位长度的速度沿AB向B运动,同时,点N从点B出发以每秒1个单位长度的速度沿BC向C运动,当点M到达B点时,两点停止运动.t为何值时,以B、M、N为顶点的三角形是等腰三角形?
(3) 点P是第一象限抛物线上的一点,若BP恰好平分∠ABC,请直接写出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家为迎接“10周年购物狂欢节”,准备将编号为l号,2号,…,60号的奖券分别对应60份奖品.现将奖券不均匀分配放置在![]() ,
,![]() ,
,![]() 三个抽奖盒中,若将
三个抽奖盒中,若将![]() 盒中的26号奖券调换到
盒中的26号奖券调换到![]() 盒,将
盒,将![]() 盒中的44号奖券调换到
盒中的44号奖券调换到![]() 盒,此时,
盒,此时,![]() 、
、![]() 两盒奖券的编号平均数比调换前增加了0.6,
两盒奖券的编号平均数比调换前增加了0.6,![]() 盒奖券的编号平均数比调换前增加了0.9,同时经计算发现,
盒奖券的编号平均数比调换前增加了0.9,同时经计算发现,![]() 盒中编号平均数调换前低于36,调换后编号平均数却高于36,则调换前
盒中编号平均数调换前低于36,调换后编号平均数却高于36,则调换前![]() 盒中有_________张奖券.
盒中有_________张奖券.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请直接写出m的值为_________.
(2)求出这个二次函数的解析式.
(3)当![]() 时,则y的取值范围为______________________________.
时,则y的取值范围为______________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,H为射线OA上一定点,
,H为射线OA上一定点,![]() ,P为射线OB上一点,M为线段OH上一动点,连接PM,满足
,P为射线OB上一点,M为线段OH上一动点,连接PM,满足![]() 为钝角,以点P为中心,将线段PM顺时针旋转
为钝角,以点P为中心,将线段PM顺时针旋转![]() ,得到线段PN,连接ON.
,得到线段PN,连接ON.
(1)依题意补全图1;
(2)求证:![]() ;
;
(3)点M关于点H的对称点为Q,连接QP.写出一个OP的值,使得对于任意的点M总有ON=QP,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.

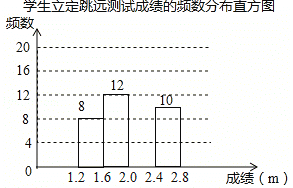
请根据图表中所提供的信息,完成下列问题:
(1)表中![]() ________,
________,![]() ________,样本成绩的中位数落在证明见解析________范围内;
________,样本成绩的中位数落在证明见解析________范围内;
(2)请把频数分布直方图补充完整;
(3)该校九年级共有1000名学生,估计该年级学生立定跳远成绩在![]() 范围内的学生有多少人?
范围内的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com