
分析 观察题中已知:是从1开始的奇数求和,结果为自然数的平方,若算式的最后一个为2n+1,结果恰是(n+1)2,由此可以求解.
解答 解:已知是从1开始的奇数求和,结果为自然数的平方,若算式的最后一个为2n+1,结果恰是(n+1)2;
1+3+5+7+9+…+13=72=49;
1+3+5+7+9+…+(2n-1)+(2n+1)=(n+1)2;
41+43+45+…+77+79=1+3+5+7+9+…+77+79-(1+3+5+7+9+…+39)=402-202=1200.
故答案为:49,(n+1)2,1200.
点评 此题主要考查数列的规律探索与运用,观察已知找到存在的规律,并准确应用是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | a=5 | B. | a=-5 | C. | a=$\frac{1}{5}$ | D. | a=-$\frac{1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $x-\frac{1}{2}y$ | B. | $\frac{3}{7}x$ | C. | $\frac{1}{x-1}$ | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
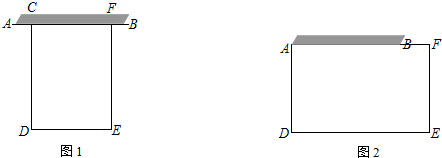
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
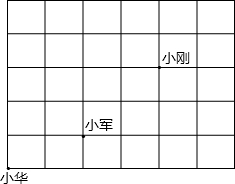 课间操时小华、小军、小刚的位置如图所示,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么小刚的位置可以用坐标表示成(4,3).
课间操时小华、小军、小刚的位置如图所示,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么小刚的位置可以用坐标表示成(4,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com