
 (k>0)上的点,分别经过A、B两点向x轴、y轴作垂线段AC、AD、BE、BF,AC和BF交于点G,得到正方形OCGF(阴影部分),且S阴影=1,△AGB的面积为2.
(k>0)上的点,分别经过A、B两点向x轴、y轴作垂线段AC、AD、BE、BF,AC和BF交于点G,得到正方形OCGF(阴影部分),且S阴影=1,△AGB的面积为2.
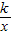 上的点,得出点A的纵坐标与点B的横坐标都是k,从而可用含k的代数式表示AG,BG,再根据△AGB的面积为2,列出关于k的方程,求解即可;
上的点,得出点A的纵坐标与点B的横坐标都是k,从而可用含k的代数式表示AG,BG,再根据△AGB的面积为2,列出关于k的方程,求解即可; AG•BG,所以本题即求
AG•BG,所以本题即求 AG•BG的值是否为一个常数.为此,设矩形OCGF的边OC=m,则点A的横坐标为m,由S阴影=OC•OF=1,可知OF=
AG•BG的值是否为一个常数.为此,设矩形OCGF的边OC=m,则点A的横坐标为m,由S阴影=OC•OF=1,可知OF= ,即点B纵坐标为
,即点B纵坐标为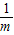 .然后由点A、B是双曲线y=
.然后由点A、B是双曲线y=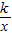 上的点,得出点A的纵横坐标与点B的横坐标,从而可用含m的代数式表示AG,BG,进而求出
上的点,得出点A的纵横坐标与点B的横坐标,从而可用含m的代数式表示AG,BG,进而求出 AG•BG的值,从而得出结果.
AG•BG的值,从而得出结果.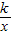 上的点,
上的点,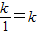 ,点B横坐标为x=
,点B横坐标为x=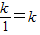 ,
, AG•BG=
AG•BG=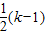 2=2,
2=2,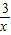 ;
;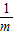 .
.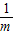 .
.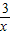 上的点,
上的点,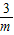 ,点B横坐标为
,点B横坐标为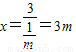 .
.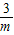 ,BF=3m.
,BF=3m.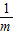 ,
,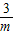 -
-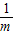 =
=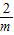 ,BG=BF-FG=3m-m=2m,
,BG=BF-FG=3m-m=2m, AG•BG=
AG•BG= •
•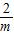 •2m=2.
•2m=2.

科目:初中数学 来源:2010年广东省汕头市潮阳区中考数学模拟试卷(解析版) 题型:填空题
 x
x 分别与x轴、y轴交于点C和点D,一组抛物线的顶点A1,A2,A3,…,An,依次是直线CD上的点,这组抛物线与x轴的交点依次是B1,B2,B3,…,Bn-1,Bn,且OB1=B1B2=B2B3=…=Bn-1Bn,点A1坐标(1,1),则点An坐标为 .
分别与x轴、y轴交于点C和点D,一组抛物线的顶点A1,A2,A3,…,An,依次是直线CD上的点,这组抛物线与x轴的交点依次是B1,B2,B3,…,Bn-1,Bn,且OB1=B1B2=B2B3=…=Bn-1Bn,点A1坐标(1,1),则点An坐标为 .
查看答案和解析>>
科目:初中数学 来源:2010年广东省汕头市潮阳区中考数学模拟试卷(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2010年广东省汕头市潮阳区中考数学模拟试卷(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com