
如图,E、F分别为线段AC上的两个动点,且DE⊥AC于点E,BF⊥AC于点F.若AB=CD,AF=CE,BD交AC于点M.
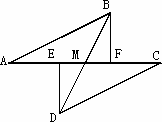
(1)求证:MB=MD,ME=MF;
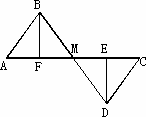
(2)当E、F两点移动至如图所示的位置,其余条件不变时,上述结论是否成立?只需作出判断即可.
 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
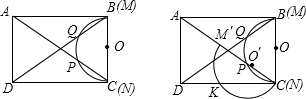 C的中点,此时量角器的半圆弧交DC于K,若K点的度数为z,那么z与y的数量关系是什么,请说明理由;
C的中点,此时量角器的半圆弧交DC于K,若K点的度数为z,那么z与y的数量关系是什么,请说明理由;查看答案和解析>>
科目:初中数学 来源: 题型:
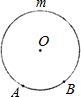 如图,A、B为⊙O上两点,下列寻找弧AB的中点C的方法中正确的有( )
如图,A、B为⊙O上两点,下列寻找弧AB的中点C的方法中正确的有( )查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,P是∠BAC平分线上一点,PD⊥AC,垂足为D,以P为圆心,PD为半径作圆.
如图,P是∠BAC平分线上一点,PD⊥AC,垂足为D,以P为圆心,PD为半径作圆.查看答案和解析>>
科目:初中数学 来源: 题型:013
[ ]
A.8° B.10° C.26° D.34°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com