
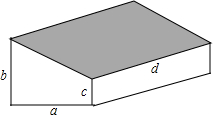
 如图,要修建一个蔬菜大棚,棚的横截面是直角梯形,棚宽a=6米,棚高分别为b=5米,c=2米,长为d=30米,现要在棚顶覆盖塑料膜(即图中阴影部分),求共计需要塑料膜多少平方米?
如图,要修建一个蔬菜大棚,棚的横截面是直角梯形,棚宽a=6米,棚高分别为b=5米,c=2米,长为d=30米,现要在棚顶覆盖塑料膜(即图中阴影部分),求共计需要塑料膜多少平方米?  名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
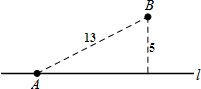 如图,一条笔直的公路l穿过草原,公路边有一消防站A,距离公路5千米的地方有一居民点B,A、B的直线距离是13千米.一天,居民点B着火,消防员受命欲前往救火,若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过$\frac{5\sqrt{3}+12}{80}$小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.)
如图,一条笔直的公路l穿过草原,公路边有一消防站A,距离公路5千米的地方有一居民点B,A、B的直线距离是13千米.一天,居民点B着火,消防员受命欲前往救火,若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过$\frac{5\sqrt{3}+12}{80}$小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线y=mx2-2mx+m+4与y轴交于点A(0,3),与x轴交于点B,C(点B在点C左侧).
在平面直角坐标系xOy中,抛物线y=mx2-2mx+m+4与y轴交于点A(0,3),与x轴交于点B,C(点B在点C左侧).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
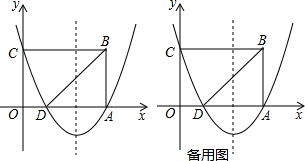
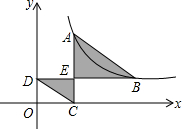 如图,点A,B在反比例函数y=$\frac{k}{x}$(x>0)的图象中,AC⊥x轴于点C,BD⊥y轴于点D,交AC于点F,连接AB,CD,若图中的阴影部分的面积和为5,且AE=2CE,则k的值为( )
如图,点A,B在反比例函数y=$\frac{k}{x}$(x>0)的图象中,AC⊥x轴于点C,BD⊥y轴于点D,交AC于点F,连接AB,CD,若图中的阴影部分的面积和为5,且AE=2CE,则k的值为( )| A. | 5 | B. | 6 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示的函数图象反映的过程是:小明从家去书店看一会儿书,又去学校取封信后马上回家,其中x表示时间(单位:小时),y表示小明离家的距离(单位:千米),则小明从学校回家的平均速度为6千米∕小时.
如图所示的函数图象反映的过程是:小明从家去书店看一会儿书,又去学校取封信后马上回家,其中x表示时间(单位:小时),y表示小明离家的距离(单位:千米),则小明从学校回家的平均速度为6千米∕小时.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com