
 ��ƽ��ֱ������ϵxOy�У�������y=mx2-2mx+m+4��y�ύ�ڵ�A��0��3������x�ύ�ڵ�B��C����B�ڵ�C��ࣩ��
��ƽ��ֱ������ϵxOy�У�������y=mx2-2mx+m+4��y�ύ�ڵ�A��0��3������x�ύ�ڵ�B��C����B�ڵ�C��ࣩ������ ��1����A�������������m��ֵ������������ߵı���ʽ����y=0�����B��C��������ꣻ
��2���ɣ�1������������ߵĶԳ��ᣬ�����D�����꣬�����ô���ϵ���������ֱ��DE�ı���ʽ��
��3����������֪��ֱ�ߺ������ߵ�ͼ���ܶ���x���Ϸ������ֱ�ߺ������ߵ�ͼ������t�ķ�Χ��
��� �⣺��1����������y=mx2-2mx+m+4��y�ύ�ڵ�A��0��3����
��m+4=3��
��m=-1��
�������ߵı���ʽΪy=-x2+2x+3��
��������y=-x2+2x+3��x�ύ�ڵ�B��C��
����y=0����-x2+2x+3=0��
��� x1=-1��x2=3��
�֡ߵ�B�ڵ�C��࣬
���B��������-1��0������C��������3��0����
��2����y=-x2+2x+3=-��x-1��2+4��
�������ߵĶԳ���Ϊֱ��x=1��
�������ߵĶԳ�����x�ύ�ڵ�D��
���D��������1��0����
��ֱ��y=kx+b������D��1��0���͵�E��-1��-2����
��$\left\{\begin{array}{l}k+b=0\\-k+b=-2.\end{array}\right.$
���$\left\{\begin{array}{l}k=1\\ b=-1.\end{array}\right.$
��ֱ��DE�ı���ʽΪy=x-1��
��3����ͼ����P����D��B����֮��ʱ��M��N����x���Ϸ���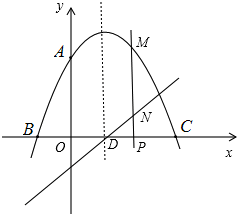
���M��N������һ������x���·���t�ķ�ΧΪ��t��1��t��3��
���� ������Ҫ������κ�����һ�κ������ۺϣ��ڣ�1����ע�����ϵ������Ӧ�ã��ڣ�2�������D�������ǽ���Ĺؼ����ڣ�3����ע�����ν��˼���Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ƽ���� | B�� | ���� | C�� | ��λ�� | D�� | ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
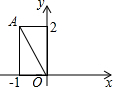 ��ͼ����֪��A��-1��2�������߶�OA��O��˳ʱ�뷽����ת90��õ��߶�OA�䣬���A��������ǣ�������
��ͼ����֪��A��-1��2�������߶�OA��O��˳ʱ�뷽����ת90��õ��߶�OA�䣬���A��������ǣ�������| A�� | ��-3��-2�� | B�� | ��2��2�� | C�� | ��3��0�� | D�� | ��2��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
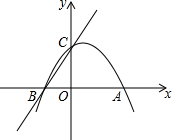 ��ͼ��ʾ�����κ���y1=-x2+nx+m��ͼ����x���һ������ΪA��3��0������һ������ΪB������y�ύ�ڵ�C��0��3����
��ͼ��ʾ�����κ���y1=-x2+nx+m��ͼ����x���һ������ΪA��3��0������һ������ΪB������y�ύ�ڵ�C��0��3�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪������x��һԪ���η���ax2-2��a-1��x+a-2=0��a��0����
��֪������x��һԪ���η���ax2-2��a-1��x+a-2=0��a��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ̨����һ����Ȼ�ֺ�������̨������ΪԲ������ʮǧ��Χ���γ������籩���м�ǿ���ƻ�����������۲죬���غ�ij����A����256ǧ��B����һ̨�����ģ�������������Ϊ12����ÿԶ��̨������20ǧ�ף������ͻ����һ������̨����������15ǧ��/ʱ���ٶ��ر�ƫ��30�㷽����C�ƶ�����̨�����ķ������䣬�������ܵ��ķ����ﵽ���ļ��������̨��Ӱ�죮
̨����һ����Ȼ�ֺ�������̨������ΪԲ������ʮǧ��Χ���γ������籩���м�ǿ���ƻ�����������۲죬���غ�ij����A����256ǧ��B����һ̨�����ģ�������������Ϊ12����ÿԶ��̨������20ǧ�ף������ͻ����һ������̨����������15ǧ��/ʱ���ٶ��ر�ƫ��30�㷽����C�ƶ�����̨�����ķ������䣬�������ܵ��ķ����ﵽ���ļ��������̨��Ӱ�죮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
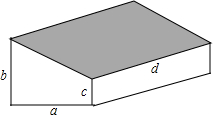 ��ͼ��Ҫ��һ���߲˴����ĺ������ֱ�����Σ����a=6�ף���߷ֱ�Ϊb=5�ף�c=2�ף���Ϊd=30�ף���Ҫ���ﶥ��������Ĥ����ͼ����Ӱ���֣�������Ҫ����Ĥ����ƽ���ף�
��ͼ��Ҫ��һ���߲˴����ĺ������ֱ�����Σ����a=6�ף���߷ֱ�Ϊb=5�ף�c=2�ף���Ϊd=30�ף���Ҫ���ﶥ��������Ĥ����ͼ����Ӱ���֣�������Ҫ����Ĥ����ƽ���ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com