
【题目】在平面直角坐标系中,抛物线![]() 顶点为
顶点为![]() .
.
(1)![]() 点坐标为______(结果用
点坐标为______(结果用![]() 表示).
表示).
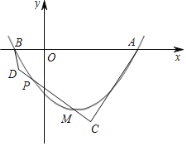
(2)当![]() 时,如图所示,该抛物线与
时,如图所示,该抛物线与![]() 轴交于
轴交于![]() ,
,![]() 两点.
两点.![]() 为抛物线第二象限一点,过
为抛物线第二象限一点,过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,![]() 为射线
为射线![]() 上一点,若
上一点,若![]() ,求
,求![]() ;
;
(3)![]() ,
,![]() ,若该抛物线与线段
,若该抛物线与线段![]() 只有一个公共点,求
只有一个公共点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)化成顶点式即可求得;
(2)过B点作BN⊥CD,交CD的延长线于N,连接BM、AM,求得点A,B,M的坐标,根据勾股定理的逆定理证得△ABM是等腰直角三角形,进而证得△AMC≌△MBN,即可证得BN=DN,得出△BDN是等腰直角三角形,根据三角形外角的性质即可求得∠BDM=135°;
(3)根据题意得到线段GH:![]() ,与
,与![]() 联立得到
联立得到![]() 令y′=
令y′=![]() ,若抛物线y=
,若抛物线y=![]() 与线段GH只有1个公共点,从而得到结论.
与线段GH只有1个公共点,从而得到结论.
(1)∵抛物线![]()
![]() ,
,
∴顶点为![]() 为
为![]() ,故答案为
,故答案为![]() ;
;
(2)过![]() 点作
点作![]() ,交
,交![]() 的延长线于
的延长线于![]() ,连接
,连接![]() 、
、![]() ,
,
∵![]() 是抛物线的顶点,
是抛物线的顶点,
∴![]() ,
,
当![]() 时,抛物线为
时,抛物线为![]() ,
,
令![]() ,则
,则![]() ,解得
,解得![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
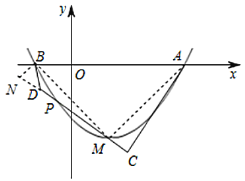
在![]() 和
和![]() 中
中
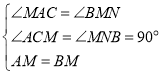
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∴![]()
![]() ;
;
(3)∵![]() ,
,![]() ,
,
∴线段![]() 为
为![]() ,
,
与![]() 联立得:
联立得:![]() ,
,
令![]() ,
,
若抛物线![]() 与线段
与线段![]() 只有1个公共点,
只有1个公共点,
即函数![]() 在
在![]() 范围内只有一个零点,
范围内只有一个零点,
当![]() 时,
时,![]() ,
,
∵![]() ,∴此种情况不存在,
,∴此种情况不存在,
当![]() 时,
时,![]() ,
,
解得![]() .
.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
【题目】在某市举办的“划龙舟,庆端午”比赛中,甲、乙两队在比赛时的路程![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系图象如图所示,根据图象得到下列结论,其中错误的是( )
(分钟)之间的函数关系图象如图所示,根据图象得到下列结论,其中错误的是( )

A.这次比赛的全程是500米
B.乙队先到达终点
C.比赛中两队从出发到1.1分钟时间段,乙队的速度比甲队的速度快
D.乙与甲相遇时乙的速度是375米/分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
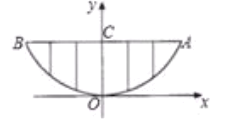
【题目】某校的围墙上端由- -段段相同的凹曲拱形栅栏组成,如图所示,栅栏的跨径![]() 间,按相同的间距
间,按相同的间距![]() 米用
米用![]() 根立柱加固,拱高
根立柱加固,拱高![]() 为
为![]() 米,以
米,以![]() 为原点,
为原点,![]() 所在的直线为
所在的直线为![]() 轴建立平面直角坐标系,根据以上的数据,则这段栅栏所需立柱的总长度(精确到
轴建立平面直角坐标系,根据以上的数据,则这段栅栏所需立柱的总长度(精确到![]() 米)为( )
米)为( )
A. ![]() 米B.
米B. ![]() 米C.
米C. ![]() 米D.
米D. ![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
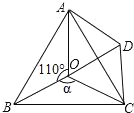
(1)试说明△COD是等边三角形;
(2)当a=150°时,OB=3,OC=4,试求OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小南利用几何画板画图,探索结论,他先画∠MAN=90°,在射线AM上取一点B,在射线AN上取一点C,连接BC,再作点A关于直线BC的对称点D,连接AD、BD,得到如图所示图形,移动点C,小南发现:当AD=BC时,∠ABD=90°;请你继续探索;当2AD=BC时,∠ABD的度数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B两点的坐标分别为A(0,2![]() ),B(2,0),直线AB与反比例函数y=
),B(2,0),直线AB与反比例函数y=![]() 的图象交于点C和点D(﹣1,a).
的图象交于点C和点D(﹣1,a).
(1)求直线AB和反比例函数的解析式;
(2)求∠ACO的度数.
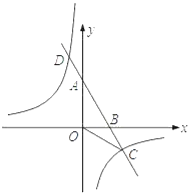
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村2016年的人均收入为20000元,2018年的人均收入为24200元
(1)求2016年到2018年该村人均收入的年平均增长率;
(2)假设2019年该村人均收入的增长率与前两年的年平均增长率相同,请你预测2019年村该村的人均收入是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从下列4个函数:①y=3x﹣2;②y=![]() (x<0);③y=
(x<0);③y=![]() (x>0);④y=﹣x2(x<0)中任取一个,函数值y随自变量x的增大而增大的概率是( )
(x>0);④y=﹣x2(x<0)中任取一个,函数值y随自变量x的增大而增大的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边AD⊥EF,垂足为点E,点H是菱形ABCD的对称中心.若FC=![]() ,EF=
,EF=![]() DE,则菱形ABCD的边长为( )
DE,则菱形ABCD的边长为( )
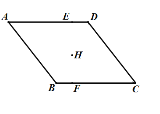
A.![]() B.3C.4D.5
B.3C.4D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com