
【题目】如图所示,直线![]() 交
交![]() 轴于点
轴于点![]() ,在
,在![]() 轴正方向上取点
轴正方向上取点![]() ,使
,使![]() ;过点
;过点![]() 作
作![]() 轴,交
轴,交![]() 于点
于点![]() ,在
,在![]() 轴正方向上取点
轴正方向上取点![]() ,使
,使![]() ;过点
;过点![]() 作
作![]() 轴,交
轴,交![]() 于点
于点![]() ,…记
,…记![]() 面积为
面积为![]() ,
,![]() 面积为
面积为![]() ,
,![]() 面积为
面积为![]() ,…,则
,…,则![]() 等于( )
等于( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
根据已知条件得到△△OA1B1,△B1A2B2,△B2A3B3是等腰直角三角形,根据最新的解析式得到A1(0,1),求得B1(1,0),得到OB1=OA1=1,根据三角形的面积公式得到S1=![]() ×1×1=
×1×1=![]() ×12,同理S2=
×12,同理S2=![]() ×2×2=
×2×2=![]() ×22,S3=
×22,S3=![]() ×4×4=
×4×4=![]() ×42;…得到Sn=
×42;…得到Sn=![]() ×22n-2=22n-3,于是得到结论.
×22n-2=22n-3,于是得到结论.
∵OB1=OA1;过点B1作A2B1⊥x轴,B1B2=B1A2;A3B2⊥x轴,B2B3=B2A3;…
∴△△OA1B1,△B1A2B2,△B2A3B3是等腰直角三角形,
∵y=x+1交y轴于点A1,
∴A1(0,1),
∴B1(1,0),
∴OB1=OA1=1,
∴S1=![]() ×1×1=
×1×1=![]() ×12,
×12,
同理S2=![]() ×2×2=
×2×2=![]() ×22,S3=
×22,S3=![]() ×4×4=
×4×4=![]() ×42;…
×42;…
∴Sn=![]() ×22n-2=22n-3,
×22n-2=22n-3,
∴S8=22×8-3=213,
故选B.


科目:初中数学 来源: 题型:
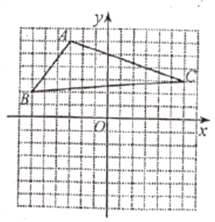
【题目】如图,![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() 、
、![]() 、
、![]() .
. ![]() 与
与![]() 关于
关于![]() 轴对称,
轴对称,![]() 与
与![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 、
、![]() 、
、![]() 分别是点
分别是点![]() 、
、![]() 、
、![]() 的对应点,点
的对应点,点![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的对应点.
的对应点.
(1)画出![]() 与
与![]() ,并写出点
,并写出点![]() 、
、![]() 、
、![]() 的坐标;
的坐标;
(2)连接![]() 、
、![]() ,求六边形
,求六边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=4,O为矩形ABCD的中心,以D为圆心1为半径作⊙D,P为⊙D上的一个动点,连接AP、OP,则△AOP面积的最大值为( )
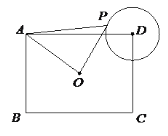
A. 4 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,点B,D在⊙O上,点E在⊙O外,∠EAB=∠D=30°.
(1)∠C的度数为 ;
(2)求证:AE是⊙O的切线;
(3)当AB=3时,求图中阴影部分的面积(结果保留根号和π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小微企业为加快产业转型升级步伐,引进一批A,B两种型号的机器.已知一台A型机器比一台B型机器每小时多加工2个零件,且一台A型机器加工80个零件与一台B型机器加工60个零件所用时间相等.
(1)每台A,B两种型号的机器每小时分别加工多少个零件?
(2)如果该企业计划安排A,B两种型号的机器共10台一起加工一批该零件,为了如期完成任务,要求两种机器每小时加工的零件不少于72件,同时为了保障机器的正常运转,两种机器每小时加工的零件不能超过76件,那么A,B两种型号的机器可以各安排多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
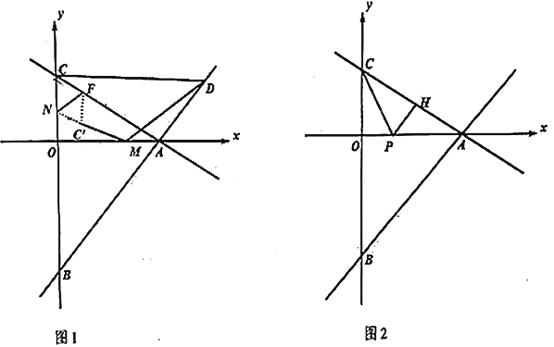
【题目】如图1,已知直线![]() 和直线
和直线![]() 交于
交于![]() 轴上一点
轴上一点![]() ,且分别交
,且分别交![]() 轴于点
轴于点![]() 、点
、点![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)如图1,点![]() 是直线
是直线![]() 上一点,且在
上一点,且在![]() 轴上方,当
轴上方,当![]() 时,在线段
时,在线段![]() 上取一点
上取一点![]() ,使得
,使得![]() ,点
,点![]() 分别为
分别为![]() 轴、
轴、![]() 轴上的动点,连接
轴上的动点,连接![]() ,将
,将![]() 沿
沿![]() 翻折至
翻折至![]() ,求
,求![]() 的最小值;
的最小值;
(3)如图2,![]() 分别为射线
分别为射线![]() 上的动点,连接
上的动点,连接![]() 是否存在这样的点
是否存在这样的点![]() ,使得
,使得![]() 为等腰三角形,
为等腰三角形,![]() 为直角三角形同时成立.请直接写出满足条件的点
为直角三角形同时成立.请直接写出满足条件的点![]() 坐标.
坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),则花园面积S的最大值为_____m2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com