【题目】（1）如图1，在Rt△ABC 中， 
，D、E是斜边BC上两动点，且∠DAE=45°，将△
绕点
逆时针旋转90后，得到△
，连接
.
（1）试说明：△
≌△
；
（2）当BE=3,CE=9时，求∠BCF的度数和DE的长；
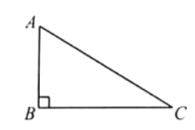
（3）如图2，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，D是斜边BC所在直线上一点，BD=3，BC=8，求DE2的长.
科目：初中数学 来源： 题型：
【题目】辰星旅游度假村有甲种风格客房15间，乙种风格客房20间．按现有定价：若全部入住，一天营业额为8500元；若甲、乙两种风格客房均有10间入住，一天营业额为5000元．
(1)求甲、乙两种客房每间现有定价分别是多少元？
(2)度假村以乙种风格客房为例，市场情况调研发现：若每个房间每天按现有定价，房间会全部住满；当每个房间每天的定价每增加20元时，就会有两个房间空闲．如果游客居住房间，度假村需对每个房间每天支出80元的各种费用．当每间房间定价为多少元时，乙种风格客房每天的利润
最大，最大利润是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，点A的坐标是（1，3），将点A绕原点O顺时针旋转90°得到点A′，则点A′的坐标是（ ）
A. （－3，1） B. （3，－1） C. （－1，3） D. （1，－3）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在等边△ABC中，D是边AC上一点，连接BD，将△BCD绕点B逆时针旋转60°，得到△BAE，连接ED，若BC＝10，BD＝9，则△ADE的周长为（ ）
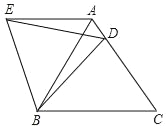
A. 19B. 20C. 27D. 30
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面是小东设计的“作矩形”的尺规作图过程，已知：
求作：矩形
作法：如图，
①作线段
的垂直平分线角交于点
；
②连接
并延长，在延长线上截取
③连接
所以四边形即为所求作的矩形
根据小东设计的尺规作图过程
（1）使用直尺和圆规，补全图形：（保留作图痕迹）
（2）完成下边的证明：
证明：
，，
四边形是平行四边形（ ）（填推理的依据）
四边形是矩形（ ）（填推理的依据）
查看答案和解析>>
科目：初中数学 来源： 题型：
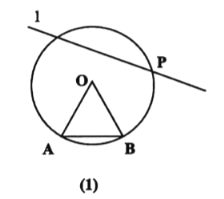
【题目】（一）如图（1），已知圆
，点
、
在圆上，且
为等边三角形，点
为直线
与圆的一个交点.连接
，
，证明：
（方法迁移）
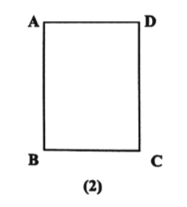
（二）如图（2），用直尺和圆规在矩形
内作出所有的点，使得
（不写作法，保留作图痕迹）.
（深入探究）
（三）已知矩形，
，
，为
边上的点，若满足的点P恰有两个，求
的取值范围.
（四）已知矩形，
，
，为矩形内一点，且
，若点绕点逆时针旋转
到点
，求
的最小值，并求此时
的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，如图1，二次函数y＝ax2+2ax﹣3a（a≠0）图象的顶点为C与x轴交于A、B两点（点A在点B左侧），点C、B关于过点A的直线l：y＝kx+
对称．
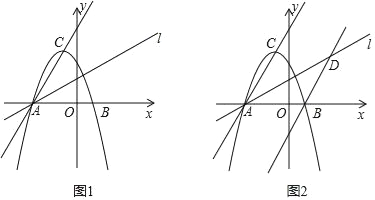
（1）求A、B两点坐标及直线l的解析式；
（2）求二次函数解析式；
（3）如图2，过点B作直线BD∥AC交直线l于D点，M、N分别为直线AC和直线l上的两个动点，连接CN，MM、MD，求CN+NM+MD的最小值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
