
【题目】如图,![]() , AD、BD、CD分别平分
, AD、BD、CD分别平分![]() 外角
外角![]() 、内角
、内角![]() 、外角
、外角![]() .以下结论:①
.以下结论:①![]() :②
:②![]() ;③
;③![]() ;④
;④![]() :⑤
:⑤![]() .其中正确的结论有( )
.其中正确的结论有( )
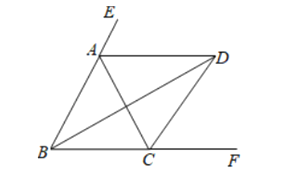
A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
根据角平分线定义得出∠ABC=2∠ABD=2∠DBC,∠EAC=2∠EAD,∠ACF=2∠DCF,根据三角形的内角和定理得出∠BAC+∠ABC+∠ACB=180°,根据三角形外角性质得出∠ACF=∠ABC+∠BAC,∠EAC=∠ABC+∠ACB,根据已知结论逐步推理,即可判断各项.
解:∵AD平分∠EAC,
∴∠EAC=2∠EAD,
∵∠EAC=∠ABC+∠ACB,∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,∴①正确;
∵AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,∠ABC=∠ACB,
∴∠ABC=∠ACB=2∠DBC,
∴∠ACB=2∠ADB,∴②正确;
∵AD平分∠EAC,CD平分∠ACF,
∴∠DAC=![]() ∠EAC,∠DCA=
∠EAC,∠DCA=![]() ∠ACF,
∠ACF,
∵∠EAC=∠ACB+∠ACB,∠ACF=∠ABC+∠BAC,∠ABC+∠ACB+∠BAC=180°,
∴∠ADC=180°-(∠DAC+∠ACD)
=180°-![]() (∠EAC+∠ACF)
(∠EAC+∠ACF)
=180°-![]() (∠ABC+∠ACB+∠ABC+∠BAC)
(∠ABC+∠ACB+∠ABC+∠BAC)
=180°-![]() (180°-∠ABC)
(180°-∠ABC)
=90°-![]() ∠ABC,∴③正确;
∠ABC,∴③正确;
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵∠ADB=∠DBC,∠ADC=90°-![]() ∠ABC,
∠ABC,
∴∠ADB不等于∠CDB,∴④错误;
∵AD∥BC,
∴∠ADC=∠DCF,
∵BD平分∠ABC,
∴![]() ∠ABC=∠DBC,
∠ABC=∠DBC,
∵∠DCF=∠DBC+∠BDC,
∴∠DCF>∠DBC,
∴∠ADC>![]() ∠ABC∴⑤错误;
∠ABC∴⑤错误;
即正确的有3个,
故选:C.


科目:初中数学 来源: 题型:
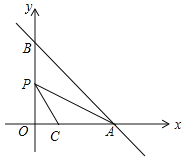
【题目】如图,在平面直角坐标系xOy中,直线y=﹣x+m分别交x轴,y轴于A,B两点,已知点C(2,0).
(1)当直线AB经过点C时,点O到直线AB的距离是 ;
(2)设点P为线段OB的中点,连结PA,PC,若∠CPA=∠ABO,则m的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明所在的学校加强学生的体育锻炼,准备从某体育用品商店一次购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买2个篮球和3个足球共需310元,购买5个篮球和2个足球共需500元.
(1)每个篮球和足球各需多少元?
(2)根据实际情况,需从该商店一次性购买篮球和足球功60个,要求购买篮球和足球的总费用不超过4000元,那么最多可以购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间,小明和父母一起开车到距家200千米的景点旅游.出发前,汽车油箱内储油45升,当行驶150千米时,发现油箱剩余油量为30升(假设行驶过程中汽车的耗油量是均匀的).
(1)求平均每千米的耗油量;
(2)如果用![]() (千米)表示行驶路程,请用含
(千米)表示行驶路程,请用含![]() 的代数式表示剩余油量;
的代数式表示剩余油量;
(3)当油箱中剩余油量低于3升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
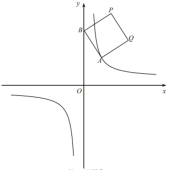
【题目】如图①,在平面直角坐标系中,![]() 是函数
是函数![]() 的图像上一点,
的图像上一点,![]() 是y轴上一动点,四边形ABPQ是正方形(点A.B.P.Q按顺时针方向排列)。
是y轴上一动点,四边形ABPQ是正方形(点A.B.P.Q按顺时针方向排列)。
(1)求a的值;
(2)如图②,当![]() 时,求点P的坐标;
时,求点P的坐标;
(3)若点P也在函数![]() 的图像上,求b的值;
的图像上,求b的值;
(4)设正方形ABPQ的中心为M,点N是函数![]() 的图像上一点,判断以点P.Q.M.N为顶点的四边形能否是正方形,如果能,请直接写出b的值,如果不能,请说明理由。
的图像上一点,判断以点P.Q.M.N为顶点的四边形能否是正方形,如果能,请直接写出b的值,如果不能,请说明理由。
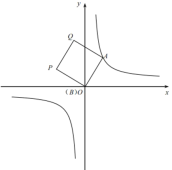
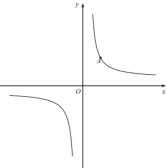
图① 图② 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是规格为![]() 正方形网格,请在所给网格中按下列要求操作:
正方形网格,请在所给网格中按下列要求操作:

(1)在网格建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2):
(2)在第二象限内的格点上画一-点C,使点C与线段AB组成一个以AB为底边的等腰三角形,且腰长是无理数.则点C坐标是____;
(3) ![]() 的周长=____ : 面积=_ 。
的周长=____ : 面积=_ 。
(4)画出![]() 关于x轴对称的
关于x轴对称的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角三角形![]() 中,
中,![]() ,
,![]() .先将
.先将![]() 绕点
绕点![]() 逆时针方向旋转
逆时针方向旋转![]() ,得到
,得到![]() ,点
,点![]() 对应点
对应点![]() ,点
,点![]() 对应点
对应点![]() ;再将
;再将![]() 沿
沿![]() 方向平移,得到
方向平移,得到![]() ,点
,点![]() 、
、![]() 、
、![]() 的对应点分别是点
的对应点分别是点![]() 、
、![]() 、
、![]() ,设平移的距离为
,设平移的距离为![]() ,且
,且![]() .
.
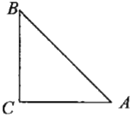
(1)在图中画出![]() 和
和![]() ;
;
(2)记![]() 与
与![]() 的交点为点
的交点为点![]() ,
,![]() 与
与![]() 的交点为点
的交点为点![]() ,如果四边形
,如果四边形![]() 的面积是
的面积是![]() 的面积的3倍,试求四边形
的面积的3倍,试求四边形![]() 和
和![]() 的面积的比值.
的面积的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中:
①0是最小的整数;
②有理数不是正数就是负数;
③正整数、负整数、正分数、负分数统称为有理数;
④非负数就是正数;
⑤![]() 不仅是有理数,而且是分数;
不仅是有理数,而且是分数;
⑥![]() 是无限不循环小数,所以不是有理数;
是无限不循环小数,所以不是有理数;
⑦无限小数不都是有理数;
⑧正数中没有最小的数,负数中没有最大的数.
其中错误的说法的个数为( )
A.7个B.6个C.5个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,点
,点![]() 在
在![]() 轴上,且
轴上,且![]() .
.
(1)求点![]() 的坐标,并画出
的坐标,并画出![]() ;
;
(2)求![]() 的面积;
的面积;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使以
,使以![]() 三点为顶点的三角形的面积为10?若存在,请直接写出点
三点为顶点的三角形的面积为10?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
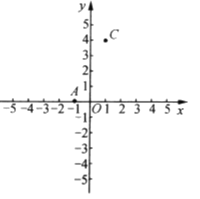
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com