
 为了美化社区环境,某小区准备对门口的一块矩形空地ABCD重新进行绿化,已知矩形的边长AB=10m,BC=20m,绿化方案如下:在矩形ABCD中间的一块四边形EFGH地面上种花,剩下的其它四块地面上铺设草坪,并要AH=CF=2AE=2CG.在满足上述条件的所有设计中,求出使四边形EFGH面积最大的AE的长和此时四边形EFGH的面积.
为了美化社区环境,某小区准备对门口的一块矩形空地ABCD重新进行绿化,已知矩形的边长AB=10m,BC=20m,绿化方案如下:在矩形ABCD中间的一块四边形EFGH地面上种花,剩下的其它四块地面上铺设草坪,并要AH=CF=2AE=2CG.在满足上述条件的所有设计中,求出使四边形EFGH面积最大的AE的长和此时四边形EFGH的面积. | 1 |
| 2 |
| 1 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 (2012•鞍山)如图,某社区有一矩形广场ABCD,在边AB上的M点和边BC上的N点分别有一棵景观树,为了进一步美化环境,社区欲在BD上(点B除外)选一点P再种一棵景观树,使得∠MPN=90°,请在图中利用尺规作图画出点P的位置(要求:不写已知、求证、作法和结论,保留作图痕迹).
(2012•鞍山)如图,某社区有一矩形广场ABCD,在边AB上的M点和边BC上的N点分别有一棵景观树,为了进一步美化环境,社区欲在BD上(点B除外)选一点P再种一棵景观树,使得∠MPN=90°,请在图中利用尺规作图画出点P的位置(要求:不写已知、求证、作法和结论,保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
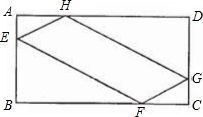 为了美化社区环境,某小区准备对门口的一块矩形空地ABCD重新进行绿化,已知矩形的边长AB=10m,BC=20m,绿化方案如下:在矩形ABCD中间的一块四边形EFGH地面上种花,剩下的其它四块地面上铺设草坪,并要AH=CF=2AE=2CG.在满足上述条件的所有设计中,求出使四边形EFGH面积最大的AE的长和此时四边形EFGH的面积.
为了美化社区环境,某小区准备对门口的一块矩形空地ABCD重新进行绿化,已知矩形的边长AB=10m,BC=20m,绿化方案如下:在矩形ABCD中间的一块四边形EFGH地面上种花,剩下的其它四块地面上铺设草坪,并要AH=CF=2AE=2CG.在满足上述条件的所有设计中,求出使四边形EFGH面积最大的AE的长和此时四边形EFGH的面积.查看答案和解析>>
科目:初中数学 来源:北京期末题 题型:解答题
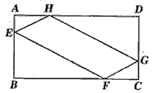
查看答案和解析>>
科目:初中数学 来源:2008-2009学年北京市朝阳区九年级(上)期末数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com