
【题目】某食品公司为迎接端午节,特别推出了几种新的粽子,并在一超市开展“品尝”活动,要求参加“品尝”活动的每一位顾客都选择一种新粽子而且只能选择一种新粽子,为了解市民对新粽子的喜欢程度,该食品公司随机抽取了参加“品尝”活动的部分顾客,进行“我最喜欢的新粽子”问卷调查,并将调查结果绘制成如下两个完整的统计图表.
参加“品尝”活动部分顾客“我最喜欢的粽子”调查结果统计表
新粽子名称 | “品尝”人数 |
香芋粽 |
|
水果粽 |
|
莲子粽 |
|
香菇粽 |
|
鲍鱼粽 |
|
火腿粽 |
|
排骨粽 |
|
参加“品尝”活动部分顾客“我最喜欢的粽子”调查结果统计表
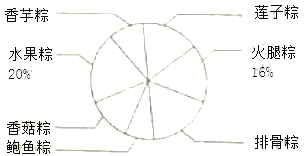
请解答下列问题:
(1)![]() _______,
_______,![]() _______.
_______.
(2)在扇形统计图中,“香芋粽”所对应的扇形圆心角为_______度.
(3)若参加“品尝”活动的顾客共有![]() 人,“品尝”某种新粽子的人数不低于
人,“品尝”某种新粽子的人数不低于![]() 人才可以批量加工,试通过计算估计该食品公司哪种新粽子不能批量加工.
人才可以批量加工,试通过计算估计该食品公司哪种新粽子不能批量加工.
【答案】(1)6,8;(2)36;(3)香芋粽、香菇粽、鲍鱼粽不能批量加工.
【解析】
(1)利用水果粽算出总数,然后利用火腿粽的百分数得到b,然后算出a;(2)算出香芋粽的百分数,进而求出圆心角;(3)算出各种粽子的人数然后进行判断
(1)总人数:10÷20%=50
火腿粽b=50×16%=8
香菇粽a=50-5-10-8-8-4-9=6
(2)香芋粽所占的百分比为5÷50=10%,所以其对应的圆心角为360°×10%=36°
(3)因为总体为样本的![]() 倍,所以可估计“品尝”各种新粽子的人数依次为:30人、60人、48人、36人、24人、48人、54人,所以香芋粽、香菇粽、鲍鱼粽不能批量加工.
倍,所以可估计“品尝”各种新粽子的人数依次为:30人、60人、48人、36人、24人、48人、54人,所以香芋粽、香菇粽、鲍鱼粽不能批量加工.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】如图,C、D为半圆上三等分点,则下列说法:①![]() =
=![]() =
=![]() ;②∠AOD=∠DOC=∠BOC;③AD=CD=OC;④△AOD沿OD翻折与△COD重合.正确的有( )
;②∠AOD=∠DOC=∠BOC;③AD=CD=OC;④△AOD沿OD翻折与△COD重合.正确的有( )
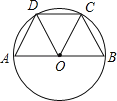
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了了解本校1200名学生的课外阅读的情况,现从各年级随机抽取了部分学生对他们一周的课外阅读时间进行了调查,并绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
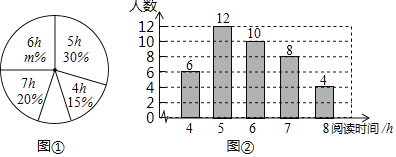
(1)本次接受随机抽样调查的学生人数为 图①中m的值为 ;
(2)本次调查获取的样本数据的众数为 ,中位数为 ;
(3)求本次调查获取的样本数据平均数;
(4)根据样本数据,估计该校一周的课外阅读时间大于6h的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⑴如图1,![]() 是正方形
是正方形![]() 边
边![]() 上的一点,连接
上的一点,连接![]() ,将
,将![]() 绕着点
绕着点![]() 逆时针旋转90°,旋转后角的两边分别与射线
逆时针旋转90°,旋转后角的两边分别与射线![]() 交于点
交于点![]() 和点
和点![]() .
.
①线段![]() 和
和![]() 的数量关系是 ;
的数量关系是 ;
②写出线段![]() 和
和![]() 之间的数量关系.
之间的数量关系.
⑵当四边形![]() 为菱形,
为菱形,![]() ,点
,点![]() 是菱形
是菱形![]() 边
边![]() 所在直线上的一点,连接
所在直线上的一点,连接![]() ,将
,将![]() 绕着点
绕着点![]() 逆时针旋转120°,旋转后角的两边分别与射线
逆时针旋转120°,旋转后角的两边分别与射线![]() 交于点
交于点![]() 和点
和点![]() .
.
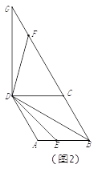
①如图2,点![]() 在线段上时,请探究线段
在线段上时,请探究线段![]() 和
和![]() 之间的数量关系,写出结论并给出证明;
之间的数量关系,写出结论并给出证明;
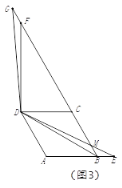
②如图3,点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() 交射线
交射线![]() 于点
于点![]() ;若
;若 ![]() ,直接写出线段
,直接写出线段![]() 的长度.
的长度.
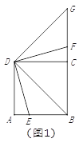
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习一定要讲究方法,比如有效的预习可大幅提高听课效率.九年级(1)班学习兴趣小组为了了解全校九年级学生的预习情况,对该校九年级学生每天的课前预习时间(单位:![]() )进行了抽样调查.并将抽查得到的数据分成5组,下面是未完成的频数、顿率分布表和频数分布扇形图.
)进行了抽样调查.并将抽查得到的数据分成5组,下面是未完成的频数、顿率分布表和频数分布扇形图.
组别 | 课前预习时间 | 频数(人数) | 频率 |
1 |
| 2 | |
2 |
|
| 0.10 |
3 |
| 16 | 0.32 |
4 |
|
|
|
5 |
| 3 |
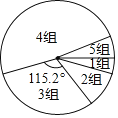
请根据图表中的信息,回答下列问题:
(1)本次调查的样本容量为 ,表中的![]() ,
,![]() ,
,![]() ;
;
(2)试计算第4组人数所对应的扇形圆心角的度数;
(3)该校九年级其有1000名学生,请估计这些学生中每天课前预习时间不少于![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,若∠DHO=20°,则∠ADC的度数是( )
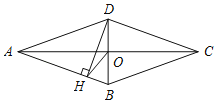
A. 120°B. 130°C. 140°D. 150°
查看答案和解析>>
科目:初中数学 来源: 题型:
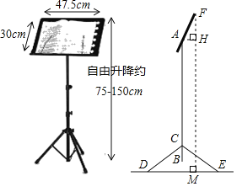
【题目】如图是小明同学的一款琴谱架,他由谱板、立杆和三角支架组成(立杆垂直于地面,三角支架的三条腿长相等),谱板的长为47.5cm,宽为30cm,在谱板长的中间,宽的下端![]() 处可调节谱板的倾斜度.如图是这款琴谱架的一种截面图.已知立杆AB=80cm,三角支架CD=30cm,CD与地面夹角∠CDE为35°,BC的长度为9cm.根据小明的身高,当谱板与水平面的夹角∠FAH调整为65°时,视谱效果最好,求此时谱板的上边沿到地面的距离FM的长.(结果精确到1cm.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin65°≈0.91,cos65°≈0.42,tan65°≈2.15)
处可调节谱板的倾斜度.如图是这款琴谱架的一种截面图.已知立杆AB=80cm,三角支架CD=30cm,CD与地面夹角∠CDE为35°,BC的长度为9cm.根据小明的身高,当谱板与水平面的夹角∠FAH调整为65°时,视谱效果最好,求此时谱板的上边沿到地面的距离FM的长.(结果精确到1cm.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin65°≈0.91,cos65°≈0.42,tan65°≈2.15)
查看答案和解析>>
科目:初中数学 来源: 题型:
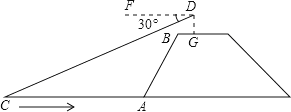
【题目】如图,兰兰站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,测得小船C的俯角是∠FDC=30°,若兰兰的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,迎水坡的坡度i=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据:![]() =1.73,结果保留两位有效数字)
=1.73,结果保留两位有效数字)
查看答案和解析>>
科目:初中数学 来源: 题型:
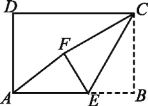
【题目】如图,在矩形ABCD中,AB=3,CB=2,点E为线段AB上的动点,将△CBE沿CE折叠,使点B落在矩形内点F处,下列结论正确的有( )
①当E为线段AB中点时,AF∥CE;②当E为线段AB中点时,AF=![]() ;③当A,F,C三点共线时,AE=
;③当A,F,C三点共线时,AE=![]() ;④当A,F,C三点共线时,△CEF≌△AEF.
;④当A,F,C三点共线时,△CEF≌△AEF.
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com