
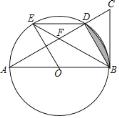
【题目】如图,以![]() 的边
的边![]() 为直径画
为直径画![]() ,交
,交![]() 于点
于点![]() ,半径
,半径![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,设
,设![]() 交
交![]() 于点
于点![]() ,若
,若![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)求出∠ADB的度数,求出∠ABD+∠DBC=90°,根据切线的判定定理即可得出结论;
(2)连接OD,分别求出三角形DOB面积和扇形DOB面积,即可求出答案.
(1)∵AB是⊙O的直径,∴∠ADB=90°,∴∠A+∠ABD=90°.
∵∠A=∠DEB,∠DEB=∠DBC,∴∠A=∠DBC.
∴∠DBC+∠ABD=90°,∴BC是⊙O的切线;
(2)连接OD.
∵BF=BC=2,且∠ADB=90°,∴∠CBD=∠FBD.
∵OE∥BD,∴∠FBD=∠OEB.
∵OE=OB,∴∠OEB=∠OBE,∴∠CBD=∠OEB=∠OBE=![]() ∠ABC=
∠ABC=![]() 90°=30°,∴∠C=60°,∴AB=
90°=30°,∴∠C=60°,∴AB=![]() BC=2
BC=2![]() ,∴⊙O的半径为
,∴⊙O的半径为![]() ,∴阴影部分的面积=扇形DOB的面积﹣三角形DOB的面积=
,∴阴影部分的面积=扇形DOB的面积﹣三角形DOB的面积=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中有三点![]() 、
、![]() 、
、![]() .请回答如下问题:
.请回答如下问题:
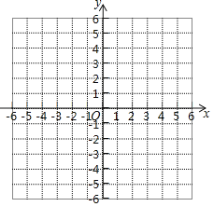
(1)在坐标系内描出![]() ;
;
(2)在坐标系中画出![]() ,使它与
,使它与![]() 关于
关于![]() 轴对称;
轴对称;
(3)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小,并求出此最小值.
的值最小,并求出此最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两位同学用围棋子做游戏.如图所示,现轮到黑棋下子,黑棋下一子后白棋再下一子,使黑棋的5个棋子组成轴对称图形,白棋的5个棋子也成轴对称图形.则下列下子方法不正确的是【 】.[说明:棋子的位置用数对表示,如A点在(6,3)]

A.黑(3,7);白(5,3) B.黑(4,7);白(6,2)
C.黑(2,7);白(5,3) D.黑(3,7);白(2,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() 是等边三角形,点
是等边三角形,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 在第一象限,
在第一象限,![]() 的平分线交
的平分线交![]() 轴于点
轴于点![]() ,把
,把![]() 绕着点
绕着点![]() 按逆时针方向旋转,使边
按逆时针方向旋转,使边![]() 与
与![]() 重合,得到
重合,得到![]() ,连接
,连接![]() .求:
.求:![]() 的长及点
的长及点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发商以20元/千克的价格购入了某种水果100千克.据市场预测,该种水果的售价y(元/千克)与保存时间x(天)的函数关系为y=30+2x,但保存这批水果平均每天将损耗10千克,且最多能保存8天.另外,批发商保存该批水果每天还需20元的费用.
(1)若批发商保存1天后将该批水果一次性卖出,则卖出时水果的售价为 (元/千克),获得的总利润为 (元);
(2)设批发商在保存了x天后一次性卖出了保存水果,获得了200元的利润,求这批水果的保存时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】六一期间,某公园游戏场举行“迎奥运”活动.有一种游戏的规则是:在一个装有![]() 个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为
个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为![]() 人次,公园游戏场发放的福娃玩具为
人次,公园游戏场发放的福娃玩具为![]() 个.
个.
![]() 求参加一次这种游戏活动得到福娃玩具的概率;
求参加一次这种游戏活动得到福娃玩具的概率;
![]() 请你估计袋中白球接近多少个?
请你估计袋中白球接近多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数![]() .
.
![]() 它的图象与二次函数
它的图象与二次函数![]() 的图象有什么关系?它是轴对称图形吗?它的开口方向,对称轴和顶点坐标分别是什么?
的图象有什么关系?它是轴对称图形吗?它的开口方向,对称轴和顶点坐标分别是什么?
![]() 当
当![]() 取哪些值时,
取哪些值时,![]() 的值随
的值随![]() 的增大而增大?当
的增大而增大?当![]() 取哪些值时,
取哪些值时,![]() 的值随
的值随![]() 的增大而减小?
的增大而减小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com