
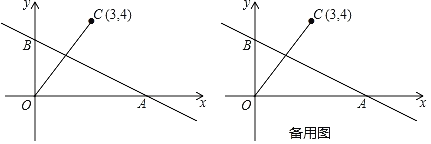
ЁОЬтФПЁПШчЭМЃЌRtЁїOABЕФжБНЧБпOAдкxжсЩЯЃЌБпOBдкyжсЩЯЃЌAЕФзјБъЮЊ(6ЃЌ0)ЃЌBЕФзјБъЮЊ(0ЃЌ3)ЃЌдкЕквЛЯѓЯогавЛЕуCЕФзјБъЮЊ(3ЃЌ4)ЃЎ
ЃЈ1ЃЉЧѓжБЯпABЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉPЪЧxжсЩЯвЛЖЏЕуЃЌЕуPдкдЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкФГИіЮЛжУЃЌЪЙЕУЁЯPBOЃНЁЯBOCЃПШєДцдкЃЌЧыЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєЖЏЕуPдкxжсЩЯДгЕу(Љ6ЃЌ0)ГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШЯђxжсе§ЗНЯђдЫЖЏЃЌЙ§ЕуPзїжБЯпlДЙжБгкxжсЃЌЩшдЫЖЏЪБМфЮЊtЃЎЧыжБНгаДГіЕБtЮЊКЮжЕЪБЃЌдкжБЯпlЩЯДцдкЕуMЃЌдкжБЯпABЩЯДцдкЕуQЃЎЪЙЕУвдOCЮЊвЛБпЃЌOЃЌCЃЌMЃЌQЮЊЖЅЕуЕФЫФБпаЮЮЊСтаЮЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉДцдкЃЌ
ЃЛЃЈ2ЃЉДцдкЃЌ![]() ЃЌ
ЃЌ![]() Лђ
Лђ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ3ЃЉ1Лђ9Лђ
ЃЛЃЈ3ЃЉ1Лђ9Лђ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈжБНгЧѓГіжБЯп![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЗжЕу![]() дк
дк![]() жсИКАыжсЪБЃЌЯШЧѓГіжБЯп
жсИКАыжсЪБЃЌЯШЧѓГіжБЯп![]() ЕФНтЮіЪНЃЌдйХаЖЯГі
ЕФНтЮіЪНЃЌдйХаЖЯГі![]() ЦНаагк
ЦНаагк![]() ЃЌНјЖјЧѓГі
ЃЌНјЖјЧѓГі![]() ЕФНтЮіЪНЃЌМДПЩЕУГіЕу
ЕФНтЮіЪНЃЌМДПЩЕУГіЕу![]() ЕФзјБъЃЌЕу
ЕФзјБъЃЌЕу![]() дк
дк![]() жсе§АыжсЪБЃЌРћгУЖдГЦадЃЌМДПЩЕУГіНсТлЃЛ
жсе§АыжсЪБЃЌРћгУЖдГЦадЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЗжвд![]() гы
гы![]() ЮЊСкБпКЭвд
ЮЊСкБпКЭвд![]() гы
гы![]() ЮЊСкБпЪБЃЌЯШЧѓГіЕу
ЮЊСкБпЪБЃЌЯШЧѓГіЕу![]() ЕФзјБъЃЌРћгУЦНвЦЕФаджЪЕУГіЕу
ЕФзјБъЃЌРћгУЦНвЦЕФаджЪЕУГіЕу![]() ЕФзјБъЃЌМДПЩЕУГіНсТлЃЎ
ЕФзјБъЃЌМДПЩЕУГіНсТлЃЎ
НтЃКЃЈ1ЃЉЩшжБЯп![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
![]() Еу
Еу![]() ЃЌ
ЃЌ![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌ
ЩЯЃЌ
![]()
![]() ЃЌ
ЃЌ
![]()
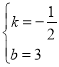 ЃЌ
ЃЌ
![]() жБЯп
жБЯп![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌ
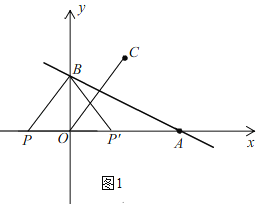
ЕБЕу![]() дк
дк![]() жсИКАыжсЩЯЪБЃЌ
жсИКАыжсЩЯЪБЃЌ
![]() Еу
Еу![]() ЃЌ
ЃЌ
![]() жБЯп
жБЯп![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() жБЯп
жБЯп![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
Сю![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
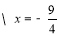 ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЕБЕу![]() дк
дк![]() жсе§АыжсЩЯЪБЃЌ
жсе§АыжсЩЯЪБЃЌ
гЩЖдГЦаджЊЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
МДЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌ
ЃЌ![]() Лђ
Лђ![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌ
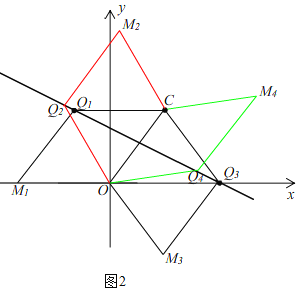
гЩЃЈ1ЃЉжЊЃЌжБЯп![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
Щш![]() ЃЌ
ЃЌ
Ђйвд![]() гы
гы![]() ЮЊСкБпЪБЃЌ
ЮЊСкБпЪБЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() Лђ
Лђ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() Еу
Еу![]() ЯђзѓЦНвЦ
ЯђзѓЦНвЦ![]() ИіЕЅЮЛЕНЕу
ИіЕЅЮЛЕНЕу![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() Еу
Еу![]() вВЯђзѓЦНвЦ5ИіЕЅЮЛЕУЕНЕу
вВЯђзѓЦНвЦ5ИіЕЅЮЛЕУЕНЕу![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() Еу
Еу![]() ЯђгвЦНвЦ
ЯђгвЦНвЦ![]() ИіЕЅЮЛЃЌдйЯђЯТЦНвЦ
ИіЕЅЮЛЃЌдйЯђЯТЦНвЦ![]() ИіЕЅЮЛЕНЕу
ИіЕЅЮЛЕНЕу![]() ЃЌ
ЃЌ
![]() Еу
Еу![]() вВЯђгвЦНвЦ3ИіЕЅЮЛЃЌдйЯђЯТЦНвЦ4ИіЕЅЮЛЕУЕНЕу
вВЯђгвЦНвЦ3ИіЕЅЮЛЃЌдйЯђЯТЦНвЦ4ИіЕЅЮЛЕУЕНЕу![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
Ђквд![]() гы
гы![]() ЮЊСкБпЪБЃЌ
ЮЊСкБпЪБЃЌ![]() ЃЌ
ЃЌ
![]()
![]() ЃЌ
ЃЌ
![]() Лђ
Лђ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() Еу
Еу![]() ЯђзѓЦНвЦ
ЯђзѓЦНвЦ![]() ИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ
ИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ![]() ИіЕЅЮЛЕНЕу
ИіЕЅЮЛЕНЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() Еу
Еу![]() вВЯђзѓЦНвЦ
вВЯђзѓЦНвЦ![]() ИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ
ИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ![]() ИіЕЅЮЛЕНЕу
ИіЕЅЮЛЕНЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() Еу
Еу![]() ЯђгвЦНвЦ
ЯђгвЦНвЦ![]() ИіЕЅЮЛЃЌдйЯђЩЯ
ИіЕЅЮЛЃЌдйЯђЩЯ![]() ИіЕЅЮЛЕН
ИіЕЅЮЛЕН![]() ЃЌ
ЃЌ
![]() Еу
Еу![]() вВЯђгвЦНвЦ
вВЯђгвЦНвЦ![]() ИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ
ИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ![]() ИіЕЅЮЛЕНЕу
ИіЕЅЮЛЕНЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
МД![]() ЕФжЕЮЊ1Лђ9Лђ
ЕФжЕЮЊ1Лђ9Лђ![]() Лђ
Лђ![]() ЃЎ
ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
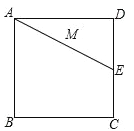
ЁОЬтФПЁПШчЙћЃЌе§ЗНаЮABCDЕФБпГЄЮЊ2cmЃЌEЮЊCDБпЩЯвЛЕуЃЌЁЯDAE=30ЁуЃЌMЮЊAEЕФжаЕуЃЌЙ§ЕуMзїжБЯпЗжБ№гыADЁЂBCЯрНЛгкЕуPЁЂQЃЌШєPQ=AEЃЌдђPDЕШгкЃЈ ЃЉ
AЃЎ![]() cmЛђ
cmЛђ![]() cm BЃЎ
cm BЃЎ![]() cm CЃЎ
cm CЃЎ![]() cmЛђ
cmЛђ![]() cm DЃЎ
cm DЃЎ![]() cmЛђ
cmЛђ![]() cm
cm
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
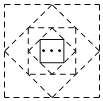
ЁОЬтФПЁПШчЭМЃЌаЁДЯгУвЛеХУцЛ§ЮЊ1ЕФе§ЗНаЮжНЦЌЃЌАДШчЯТЗНЪНВйзїЃК
ЂйНЋе§ЗНаЮжНЦЌЫФНЧЯђФкелЕўЃЌЪЙЫФИіЖЅЕужиКЯЃЌеЙПЊКѓбиелКлМєПЊЃЌАбЫФИіЕШбќжБНЧШ§НЧаЮШгЕєЃЛ
ЂкдкгрЯТжНЦЌЩЯвРДЮжиИДвдЩЯВйзїЃЌ
ЕБЭъГЩЕк2020ДЮВйзїЪБЃЌгрЯТжНЦЌЕФУцЛ§ЮЊЃЈ ЃЉ
A.22019B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
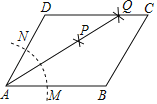
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮABCDжаЃЌАДвдЯТВНжшзїЭМЃКЂйвдAЮЊдВаФЃЌШЮвтГЄЮЊАыОЖзїЛЁЃЌЗжБ№НЛABЃЌADгкЕуMЃЌNЃЛЂкЗжБ№вдMЃЌNЮЊдВаФЃЌвдДѓгк![]() MNЕФГЄЮЊАыОЖзїЛЁЃЌСНЛЁЯрНЛгкЕуPЃЛЂлзїAPЩфЯпЃЌНЛБпCDгкЕуQЃЌШєDQ=2QCЃЌBC=3ЃЌдђЦНааЫФБпаЮABCDжмГЄЮЊ________ЃЎ
MNЕФГЄЮЊАыОЖзїЛЁЃЌСНЛЁЯрНЛгкЕуPЃЛЂлзїAPЩфЯпЃЌНЛБпCDгкЕуQЃЌШєDQ=2QCЃЌBC=3ЃЌдђЦНааЫФБпаЮABCDжмГЄЮЊ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
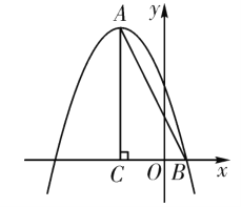
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌХзЮяЯп
ЃЌХзЮяЯп![]() ОЙ§
ОЙ§![]() СНЕуЃЎ
СНЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕу![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯЗНХзЮяЯпЩЯЕФвЛЕуЃЌЙ§Еу
ЩЯЗНХзЮяЯпЩЯЕФвЛЕуЃЌЙ§Еу![]() зї
зї![]() жсгкЕу
жсгкЕу![]() ЃЌНЛЯпЖЮ
ЃЌНЛЯпЖЮ![]() гкЕу
гкЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЎ
ЃЎ
ЂйЧѓЕу![]() ЕФзјБъКЭ
ЕФзјБъКЭ![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
ЂкдкжБЯп![]() ЩЯЪЧЗёДцдкЕу
ЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЮЊжБНЧШ§НЧаЮЃПШєДцдкЃЌжБНгаДГіЗћКЯЬѕМўЕФЫљгаЕу
ЮЊжБНЧШ§НЧаЮЃПШєДцдкЃЌжБНгаДГіЗћКЯЬѕМўЕФЫљгаЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЩНЖЅгавЛЫў![]() ЃЌЫўИп
ЃЌЫўИп![]() ЃЎМЦЛЎдкЫўЕФе§ЯТЗНбижБЯп
ЃЎМЦЛЎдкЫўЕФе§ЯТЗНбижБЯп![]() ПЊЭЈДЉЩНЫэЕР
ПЊЭЈДЉЩНЫэЕР![]() ЃЎДггы
ЃЎДггы![]() ЕуЯрОр
ЕуЯрОр![]() ЕФ
ЕФ![]() ДІВтЕУ
ДІВтЕУ![]() ЁЂ
ЁЂ![]() ЕФбіНЧЗжБ№ЮЊ
ЕФбіНЧЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЃЌДггы
ЃЌДггы![]() ЕуЯрОр
ЕуЯрОр![]() ЕФ
ЕФ![]() ДІВтЕУ
ДІВтЕУ![]() ЕФбіНЧЮЊ
ЕФбіНЧЮЊ![]() ЃЎЧѓЫэЕР
ЃЎЧѓЫэЕР![]() ЕФГЄЖШЃЎЃЈВЮПМЪ§ОнЃК
ЕФГЄЖШЃЎЃЈВЮПМЪ§ОнЃК![]() ЃЌ
ЃЌ![]() ЃЎЃЉ
ЃЎЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
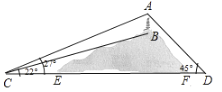
ЁОЬтФПЁПЫцзХаТХЉДхЕФНЈЩшКЭОЩГЧЕФИФдьЃЌЮвУЧЕФМвдАдНРДдНУРРіЃЌаЁУїМвИННќЙуГЁжабыаТаоСЫвЛИідВаЮХчЫЎГиЃЌдкЫЎГижааФЪњжБАВзАСЫвЛИљИп![]() УзЕФХчЫЎЙмЃЌЫќХчГіЕФХзЮяЯпаЮЫЎжљдкгыГижааФЕФЫЎЦНОрРыЮЊУзДІДяЕНзюИпЃЌЫЎжљТфЕиДІРыГижааФ
УзЕФХчЫЎЙмЃЌЫќХчГіЕФХзЮяЯпаЮЫЎжљдкгыГижааФЕФЫЎЦНОрРыЮЊУзДІДяЕНзюИпЃЌЫЎжљТфЕиДІРыГижааФ![]() Уз.
Уз.

ЃЈ1ЃЉЧыФуНЈСЂЪЪЕБЕФжБНЧзјБъЯЕЃЌВЂЧѓГіЫЎжљХзЮяЯпЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЧѓГіЫЎжљЕФзюДѓИпЖШЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌ
ЃЌ![]() ЃЌгы
ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌжБЯп
ЃЌжБЯп![]() ЮЊ
ЮЊ![]() .
.
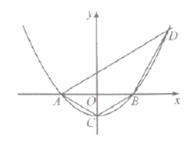
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪН.
ЃЈ2ЃЉЙ§Еу![]() зїжБЯп
зїжБЯп![]() гыХзЮяЯпдкЕквЛЯѓЯоЕФНЛЕуЮЊ
гыХзЮяЯпдкЕквЛЯѓЯоЕФНЛЕуЮЊ![]() .ЕБ
.ЕБ![]() ЪБЃЌШЗЖЈжБЯп
ЪБЃЌШЗЖЈжБЯп![]() гы
гы![]() ЕФЮЛжУЙиЯЕ.
ЕФЮЛжУЙиЯЕ.
ЃЈ3ЃЉдкЕкЖўЯѓЯоХзЮяЯпЩЯЧѓвЛЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
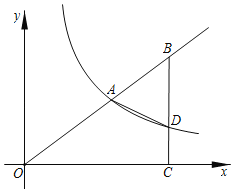
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЕу
жаЃЌЕу![]() дкЗДБШР§КЏЪ§
дкЗДБШР§КЏЪ§![]() ЕФЭМЯѓЩЯЃЌЕу
ЕФЭМЯѓЩЯЃЌЕу![]() дк
дк![]() ЕФбгГЄЯпЩЯЃЌ
ЕФбгГЄЯпЩЯЃЌ![]() жсЃЌДЙзуЮЊ
жсЃЌДЙзуЮЊ![]() ЃЌ
ЃЌ![]() гыЗДБШР§КЏЪ§ЕФЭМЯѓЯрНЛгкЕу
гыЗДБШР§КЏЪ§ЕФЭМЯѓЯрНЛгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓИУЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШє![]() ЃЌЩшЕу
ЃЌЩшЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЧѓЯпЖЮ
ЃЌЧѓЯпЖЮ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com